نواف بن حامد البحيثي
قسم الدراسات الاجتماعية ونظم المعلومات الجغرافية || كلية الآداب || شعبة الجغرافيا || جامعة الملك فيصل || الأحساء
المقدمة:
يتوقف الجريان السيلي الأحواض المائية المتحكمة على الأبعاد المورفومترية لمساحة التصريف وخصائص الشبكة المائية. ويرتبط تشابه ظروف تكوين شبكة المجاري المائية والعوامل المؤثرة في تطورها بتشابه خصائصها المورفومترية والمناخية والصخرية وبنيتها الجيولوجية وقد أشار العديد من الباحثين، إلى أن التحليل المورفومتري لعناصر الحوض المائي يساعد في دراسة العلاقات بين المتغيرات التضاريسية والعلاقات بين الخصائص الصخرية وكمية التصريف من جهة والمتغيرات المورفومترية من جهة ثانية. كما ان التحليل المورفومتري يساعد في تصنيف أحواض التصريف ذات الخصائص المتشابهة Doornkam,1971) and King).
لذا يهدف هذا البحث إلى تحليل الخصائص المورفومترية لمساحات التصريف التي يمتد عليها النطاق العمراني لمدينة حفر الباطن، وهي عشرة أحواض روافد تؤثر مباشرة على المناطق السكنية والعمرانية بالمدينة. وتتلخص المتغيرات المورفومترية التي شملها هذا البحث على مساحة التصريف ومحيط الحوض المائي وطوله ومحيطه ومتوسط عرضه، بالإضافة إلى دراسة علاقة الطول بالمساحة ونسبة معامل الشكل ونسبة الاستطالة ونسبة الاستدارة ومعامل الاندماج ومعامل الانبعاج، وايضاً دراسة العلاقات الارتباطية بين الخصائص المورفومترية. كما تتناول هذه الدراسة تحليل الخصائص التضاريسية ذات المدلول الجيومورفولوجي بأحواض التصريف الداخلة على مدينة حفر الباطن حيث شملت دراسة الارتفاعات (الأقصى، الأدنى، المتوسط) ومتوسط انحدار الحوض المائي وطول أطول مجرى مائي وانحدار خط تقسيم المياه ومتوسط انحدار أطول مجرى مائي والتضاريس النسبية ونسبة التضاريس واجمالي التضاريس والتكامل الهيبسومتري. وأيضا دراسة العلاقات الارتباطية بين المتغيرات التضاريسية. وأخيراً يتناول البحث تحليل الخصائص الهيدرولوجية لأحواض التصريف المدروسة.
مشكلة البحث:
تتعرض مدن المملكة العربية السعودية للعديد من كوارث السيول خلال السنوات الأخيرة مما الحقت اضراراً في الممتلكات العامة والخاصة. وتعد مدينة حفر الباطن احدى مدن السيول التي عانت من هذه المشكلة كونها تقع على مجرى وادي الباطن.
منهجية البحث:
يعتمد هذا البحث على المنهج الوصفي التحليلي بغرض تحديد أحواض الروافد المؤثرة على النطاق العمراني في مدينة حفر الباطن. كما يعتمد على الأسلوب الكمي من اجل تحليل المعطيات المورفومترية للأحواض المدروسة باستخدام تقنية نظم المعلومات الجغرافية. وأيضا استخدام برنامج spss في التحليل الاحصائي لدراسة العلاقات الارتباطية بين المتغيرات.
1- الخصائص الطبيعية لمنطقة الدراسة:
تقع مدينة حفر الباطن في الشمال الشرقي من المملكة العربية السعودية في محافظة حفر الباطن التابعة لإمارة المنطقة الشرقية. أما فلكياً فهي تقع بين خطي عرض 21 28و 31 28 شمالاً وخطي طول54 45و 06 46 شرقاً الشكل رقم (1). وتبلغ مساحتها 144 كم2(السرور،2007).
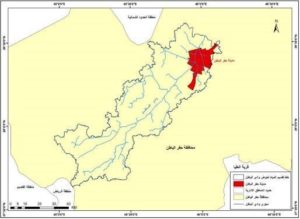
الشكل رقم (1) موقع مدينة حفر الباطن داخل حوض وادي الباطن
المصدر: عمل الباحث بالاعتماد على نموذج الارتفاع الرقمي
كما تقع على مجرى وادي الباطن رافد وادي الرمة، الذي ينبع من شرق المدينة المنورة ويمتد باتجاه الشمال الشرقي ليصل إلى صحرا الدهناء، وتغطي بعض اجزاءه بها تارة وتظهر تارة أخرى تحت الرمال المتحركة. وبعد صحراء الدهناء يواصل امتداده نحو الشمال الشرقي مجتازاً مدينة حفر الباطن وماراً بمدخلها الرئيسي في طريق الملك فيصل ثم شارع الملك عبد العزيز حتى يخرج من شمالها متجهاً نحو الشرق بمحاذاة حدود دولة الكويت ليصب في الأراضي العراقية (هيئة المساحة الجيولوجية السعودية،2012). ويعد وادي الباطن جزءاً من تضاريس الرف العربي الذي يغطي ثلثي مساحة المملكة العربية السعودية بنحو 68%. ونظراً لوقوع منطقة الدراسة ضمن نطاق المناخ المداري الصحراوي الجاف فان نظام تساقط الامطار بها يتسم بالتذبذب في الزمان والمكان (عزيز، 1972).
2- تحليل الخصائص المورفومترية:
تتأثر الخصائص المورفومترية للأحواض بالخصائص التضاريسية. والتي تؤثر بدورها على مخاطر السيول بالأحواض المائية، ويتم تحديدها بواسطة المعادلات الرياضية التي تعتمد التي تم استخلاصها من مخرجات نموذج الارتفاعات الرقمية باستخدام تطبيقات التحليل المكاني Spatial Analysis في برنامج ArcGIS.
2-1 مساحة الحوض:
تعتبر المساحة الحيز المكاني الذي تتم فيه العمليات الجيومورفولوجية من نحت ونقل وترسيب، وهي المجال الذي يتطور داخله نظام شبكة التصريف السطحي من خلال أعداد المجاري وأطوالها وكمية التصريف وكثافته (كليو، 1988 م). وتتناسب مساحة التصريف طول وعرض وطول خط تقسيم المياه للحوض المائي مع امتداد الشبكة المائية التي ترتبط بدورة وبديناميكية التعرية المائية.
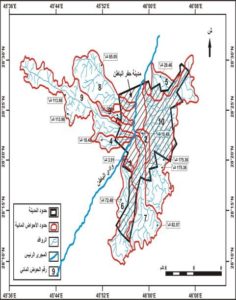
الشكل رقم (2) أحواض الروافد الداخلة على مدينة حفر الباطن
المصدر: عمل الباحث بالاعتماد على مخرجات بيانات الارتفاع الرقمي من آستر لعام2011.
وتؤثر مساحة التصريف على كمية التصريف وحجم السيول التي تتزايد مع كبر هذه المساحة مما يساعد على زيادة النشاط الجيومورفولوجي لعمليات التعرية وارتفاع درجة خطورة السيول
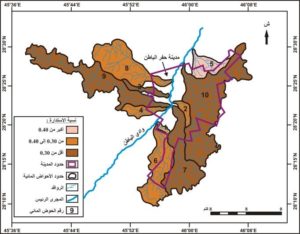
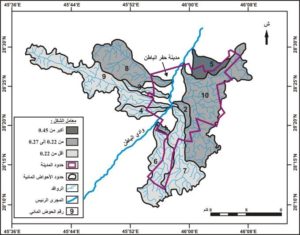
(سلامه،2004م). وبمقارنة مساحة التصريف لأحواض الروافد المدروسة نجد أن الحوض رقم 1 هو أصغر الأحواض المائية بمساحة لا تتعدى 3.91 كم2 والحوض المائي رقم 10 هو أكبر الأحواض بمساحة تصل إلى 175.36 كم2. ويمكن تصنيف أحواض الروافد المدروسة في ثلاث فئات حسب مساحة تصريفها من خلال الشكل رقم (3).
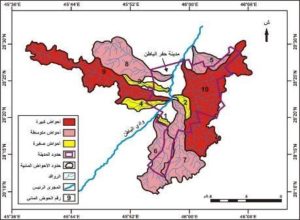
الشكل رقم (3) تصنيف أحواض الروافد المدروسة حسب المساحة
2-2 محيط الحوض:
يتأثر طول محيط الحوض المائي بشكل خط تقسيم المياه، بحيث تتزايد محيطات الأحواض التي تتسم خطوط تقسيم مياهها بتعرجات كثيرة. ويؤثر طول محيط الحوض المائي في كثير من المعاملات المورفومترية ذات المدلول الجيومورفولوجي للخصائص الشكلية لمساحة التصريف، وهو يمثل أيضاً الحدود المكانية لحوض التصريف وما يجاوره من أحواض أخرى.
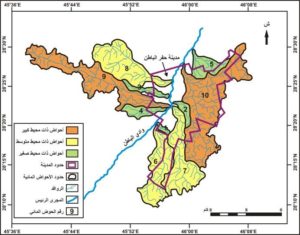
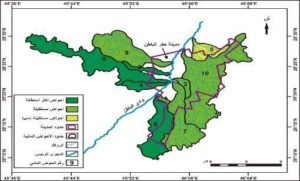
الشكل رقم (4) تصنيف أحواض الروافد المدروسة حسب طول محيط الحوض
ويستخدم طول محيط الحوض المائي في حساب العديد من المتغيرات المورفومترية باعتباره متغير مستقل واساسي مثل حساب المحيط النسبي ومعامل الاستدراة ومعامل الاندماج ونسبة الاستطالة وغيرها. ويتوافق تباين طول محيط الحوض المائي بأحواض الروافد المدروسة مع تباين مساحات تصريفها، بحيث يمكن تصنيف أحواض الروافد المدروسة إلى ثلاثة فئات اعتماداً على طول محيطها، كما يبينها الجدول رقم (2) والشكل رقم (4) وهي:
2-3 المحيط النسبي:
وضع شوم عام 1956 معادلة لحساب المحيط النسبي للحوض المائي بواسطة العلاقة النسبية بين مساحة التصريف ومحيط الحوض المائي بتطبيق المعادلة الرياضية التالية:
مساحة التصريف للحوض المائي (كم2)
المحيط النسبي
محيط الحوض المائي (كم)
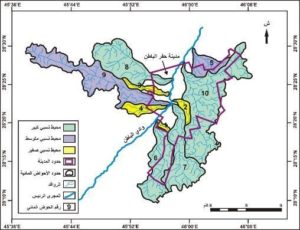
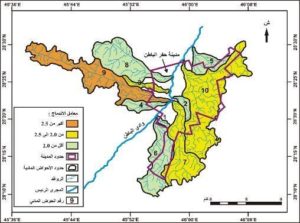
الشكل رقم (5) تصنيف أحواض الروافد المدروسة حسب المحيط النسبي
2-4 طول الحوض:
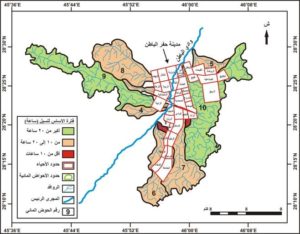
تم حساب طول أحواض الروافد المدروسة بناء على تعريف شوم من خلال استخدام أدوات التحليل المكاني في برنامج ArcGIS بحيث تتراوح أطوال الأحواض المدروسة بين 4.17 كم بالحوض (1) و35.26 كم بالحوض (9). ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاث فئات على حسب طول أحواضها كما يبينها الجدول رقم (4)و الشكل رقم (6) وهي:
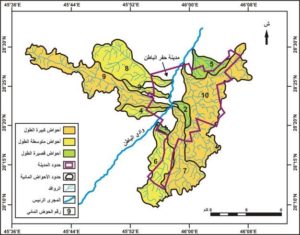
الشكل رقم (6) تصنيف أحواض الروافد المدروسة حسب طول الحوض
2-5 علاقة طول الحوض بمساحة الحوض:
علاقة طول الحوض بمساحة الحوض 1.4 (مساحة التصريف للحوض المائي(كم2))0.6
وعليه نجد أن أطوال الأحواض المدروسة المحسوبة بهذه العلاقة لا تختلف كثيراً عن الأطوال التي تم الحصول عليها بواسطة أدوات التحليل المكاني من برنامج ArcGIS بالأحواض (2، 4، 5، 7) بينما تتباين أكثر ببقية الأحواض الأخرى. ويتناسب تصنيف أحواض الروافد المدروسة اعتماداً على علاقة الطول بالمساحة مع تصنيفها اعتماداً على مساحة التصريف (الشكل3).
2-6 متوسط عرض الحوض:
هو عبارة عن العلاقة النسبية بين مساحة الحوض وطوله التي تمثلها المعادلة الرياضية التالية:
مساحة التصريف للحوض المائي (كم2)
متوسط عرض الحوض المائي
طول الحوض المائي (كم)
ويتأثر عرض الحوض المائي بزيادة أطوال المجاري المغذية للمجرى الرئيس، بحيث يتزايد امتداد عرض الحوض بالمناطق التي يتزايد بها أطوال المجاري على ضفتي الوادي الرئيس. ويرتبط عرض الحوض بنوع التكوينات الصخرية اللينة التي تساعد على امتداد أطوال المجاري المائية بسهولة على السفوح. ويتباين عرض أحواض الروافد المدروسة من حوض لآخر وهو يتراوح بين 0.94 كم بالحوض (1) و4.31 كم بالحوض (8). ويمكن تصنيف أحواض الروافد المدروسة اعتماداً على متوسط عرضها إلى ثلاث فئات كما يوضحه والشكل رقم (7) وهي:
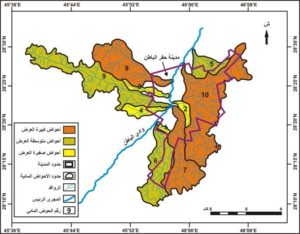
الشكل رقم (7) تصنيف أحواض الروافد المدروسة حسب متوسط عرض الحوض
2-7 معامل الشكل:
يؤثر شكل الحوض على كمية الجريان السطحي وذروة تدفق السيول بالحوض المائي. وقد وضع هورتون عام 1932 معادلة لحساب قيمة معامل شكل الحوض المائي بواسطة العلاقة النسبية بين مساحة التصريف ومربع طول الحوض المائي ويحسب بتطبيق المعادلة الرياضية التالية:
معامل الشكل
مساحة التصريف للحوض المائي (كم)
(طول الحوض المائي (كم))2
الشكل رقم (8) تصنيف أحواض الروافد المدروسة حسب معامل الشكل
وتبلغ قيمة معامل الشكل للحوض دائري الشكل تماماً 1.277 وتتناقص تدريجياً مع زيادة استطالة شكل الحوض المائي (Zavoinau, 1978,). ويتضح من خلال قيم معامل الشكل المحسوبة من معادلة هورتون أن شكل الحوض (9) هو الأكثر اختلافاً عن الشكل الدائري بمعامل شكل لا يتعدى 0.09 وأن شكل الحوض (5) هو أقرب الأشكال للشكل الدائري بمعامل شكل يصل إلى 0.46.
وعليه فإنه كلما اقترب شكل الحوض المائي من الشكل الدائري كلما ارتفعت احتمالية خطورة السيول لأن المياه الجارية تصل في أوقات متقاربة من جميع الروافد إلى المجرى الرئيس (أبو العينين، 1988) . ويمكن تصنيف أحواض الروافد المدروسة اعتماداً على معامل الشكل إلى ثلاث فئات كما يوضحه الشكل رقم (8) .
2-8 نسبة الاستطالة:
عرف شوم 1956 نسبة الاستطالة بالعلاقة النسبية بين أقصى طول للحوض المائي وقطر دائرة لها مساحة تساوي مساحة التصريف لنفس الحوض. وتحسب قيمة نسبة الاستطالة بتطبيق المعادلة الرياضية التالية:
نسبة الاستطالة 0.5
وتبلغ قيمة هذا المعامل واحد إذا كانت مساحة التصريف دائرية تماماً. ولقد اقترح شوم (1956, p. 612) تصنيفاً للأحواض المائية اعتمادا على قيمة نسبة الاستطالة بالأحواض المستديرة بنسبة استطالة تتراوح بين 0.9و 1.0و الأحواض البيضوية بنسبة استطالة تتراوح بين 0.8و 0.9و الأحواض المستطيلة نسبياً بنسبة استطالة تتراوح بين 0.7و 0.8و الأحواض المستطيلة بنسبة استطالة تتراوح بين 0.5و 0.7و الأحواض الأكثر استطالة بنسبة استطالة تقل عن 0.5.
|
الشكل رقم (9) تصنيف أحواض الروافد المدروسة حسب نسبة الاستطالة لشوم Schumm |
واعتماداً على تصنيف شوم يتبين أن هناك حوضا واحد مستطيلا نسبيا بنسبة تتراوح بين 0.7و 0.8و هو الحوض (5)، أي ما يعادل 14.8% من اجمالي نسبة الاستطالة بأحواض الروافد المدروسة. وأن الأحواض المستطيلة هي (8،10،2،7،1) بنسبة تتراوح بين 0.5 و0.7، أي ما يعادل 53.2% من إجمالي نسبة الاستطالة بأحواض الروافد المدروسة. وأن الأحواض الاكثر استطالة هي (9،6،4،3) بنسبة اقل من 0.5، أي ما يعادل 31.8% من اجمالي نسبة الاستطالة بأحواض الروافد المدروسة (الشكل رقم 9).
2- 9 نسبة الاستدارة:
اقترح ميلر سنة 1953 العلاقة النسبية بين مساحة التصريف للحوض المائي ومربع محيطه لحساب معامل الاستدارة بتطبيق المعادلة الرياضية التالية:
12.57 مساحة التصريف للحوض المائي (كم2)
نسبة الاستدارة
(محيط الحوض المائي (كم))2
|
|
الشكل رقم (10) تصنيف أحواض الروافد المدروسة حسب نسبة الاستدارة
وتبلغ قيمة هذه النسبة واحد إذا كانت مساحة التصريف دائرية تماماً. وتتباين نسبة الاستدارة بين الأحواض المدروسة وهي تتراوح بين 0.11 بالحوض (9)و 0.48 بالحوض (1) وهي تدل على استطالة خط تقسيم المياه واختلافه تماماً عن الشكل الدائري بالأحواض المدروسة. ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاث فئات على حسب نسبة الاستدارة من خلال الشكل رقم (9) وهي:
2-10 معامل الاندماج:
معامل الاندماج هو عبارة عن العلاقة النسبية بين محيط الحوض المائي ومحيط دائرة لها مساحة تساوي مساحة التصريف لنفس الحوض حسب النموذج الذي وضعه جرفيليس في سنة 1914م.
| الشكل رقم (11) تصنيف أحواض الروافد المدروسة حسب معامل الاندماج |
وتحسب قيمة معامل الاندماج بتطبيق المعادلة الرياضية التالية:
0.2841 محيط الحوض المائي (كم)
2-11 معامل الاندماج
(مساحة التصريف للحوض المائي (كم2)) 0.5
وتبلغ قيمة هذا المعامل واحد إذا كانت مساحة التصريف دائرية تماماً.
وتشير القيم المرتفعة لهذا المعامل بالأحواض المدروسة إلى استطالة خط تقسيم المياه. وتتباين قيمة معامل الاندماج بين الأحواض المدروسة وهي تتراوح بين 1.45 بالحوض (1)و 3.08 بالحوض (9). ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاث فئات اعتمادا على معامل الاندماج كما يوضحه الشكل رقم (10).
2-12 معامل الانبعاج:
يختلف شكل مساحة التصريف كثيراً عن الشكل الدائري فهي تكون عادة واسعة بالحوض العلوي وتضيق تدريجياً كما اتجهنا نحو المصب بالحوض الأدنى. ولذا اقترح شورلي عام 1957 معامل الانبعاج للتعبير عن هذا الشكل الهندسي لأحواض التصريف بتطبيق المعادلة الرياضية التالية:
3.14 (طول الحوض المائي (كم))2
معامل الانبعاج
4 مساحة التصريف للحوض المائي (كم2)
وتبلغ قيمة هذا المعامل واحد إذا كانت مساحة التصريف دائرية تماماً.
وتؤكد القيم المنخفضة لهذا المعامل استطالة الأحواض المائية المدروسة بحيث تتراوح قيمة هذا المعامل بين 0.07 بالحوض (10) و0.44 بالحوض (3). ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاث فئات اعتمادا على معامل الانبعاج كما يوضحه الجدول رقم (10) والشكل رقم (11) وهي:
 |
|
الشكل رقم (12): تصنيف أحواض الروافد المدروسة حسب معامل الانبعاج |
2-13 نسبة الطول إلى العرض:
يتشابه هذا المعامل في مدلوله الجيومورفولوجي والمورفومتري مع نسبة الاستطالة بحيث كلما كانت قيمة هذا المعامل مرتفعة كلما دلت على استطالة الحوض المائي والعكس صحيح.
الشكل رقم (13) تصنيف أحواض الروافد المدروسة حسب نسبة الطول إلى العرض
وتحسب نسبة الطول إلى العرض بتطبيق المعادلة الرياضية التالية:
طول الحوض المائي (كم)
نسبة الطول إلى العرض
عرض الحوض المائي (كم)
وتتراوح قيمة نسبة الطول إلى العرض بأحواض الروافد المدروسة بين 2.19 بالحوض (5) و10.92 بالحوض (9). ويمكن تصنيف أحواض الروافد المدروسة حسب نسبة الطول إلى العرض إلى ثلاث فئات كما يبينه الشكل رقم (13) .
– العلاقات الارتباطية بين المتغيرات المورفومترية:
تتأثر المتغيرات المورفومترية فيما بينها كما اتضح ذلك من خلال فحص علاقات الارتباط بينها بواسطة ارتباط بيرسون بحيث تبين أن هذه المتغيرات ترتبط فيما بينها بنوعين من علاقات الارتباط هي:
- علاقات ارتباط موجبة وطردية عند مستوى الدلالة 0.01 كتلك التي تربط بين نسبة الاستطالة ومعامل الشكل وبين علاقة الطول بالمساحة من جهة وكل من متوسط عرض الحوض والمحيط النسبي وطول الحوض ومحيطه ومساحة تصريفه من جهة ثانية. وبين متوسط عرض الحوض من جهة والمحيط النسبي ومحيط الحوض من جهة ثانية وبين المحيط النسبي ومساحة التصريف. وبين طول الحوض ومحيطه. وبين محيط الحوض ومساحته.
- هناك علاقات ارتباط عكسية عند مستوى الدلالة 0.01 تربط بين نسبة الطول إلى العرض من جهة ونسبة الاستطالة ومعامل الشكل من جهة ثانية. وبين معامل الانبعاج من جهة وعلاقة الطول بالمساحة ومتوسط عرض الحوض والمحيط النسبي من جهة ثانية. وبين معامل الانبعاج ونسبة الاستدارة من جهة وطول الحوض ومحيطه من جهة ثانية.
- كما أن هناك علاقات ارتباط طردية بين المتغيرات المورفومترية عند مستوى الدلالة 0.05 تربط بين معامل الاندماج من جهة ونسبة الطول إلى العرض ومساحة الحوض من جهة ثانية. وبين المحيط النسبي من جهة وطول الحوض ومحيطه من جهة ثانية.
- في حين هناك مجموعة من الارتباطات العكسية عند مستوى الدلالة 0.05 تربط بين معامل الانبعاج من جهة وطول الحوض ومساحته ومحيطه من جهة ثانية. وبين نسبة الاستدارة من جهة ونسبة الطول إلى المساحة ومساحة الحوض من جهة ثانية.
3- تحليل الخصائص التضاريسية:
تبرز أهمية دراسة الخصائص التضاريسية وتحليل تبايناتها المكانية فيما يترتب عنها من ظاهرات جيومورفولوجية (أشكال التعرية) تؤثر بدورها على كمية التصريف واتجاه الجريان السطحي الذي يحدث من فترة لأخرى خلال فترات تساقط الأمطار (جاد، 1980). ويتأثر الجريان السطحي بخصائص الحوض المائي خاصة عاملي الارتفاع والانحدار.. كما ترتبط الطاقة الكامنة لعمليات التعرية وحركة المياه والرواسب داخل الحوض المائي بالخصائص التضاريسية، بحيث توصل شوم إلى وجود علاقات طردية بين معدل التعرية ودرجة الانحدار لسطح التضاريس بالأحواض المائية((Schumm, 1977. ولذا يتأثر ظهور الجريان السطحي بعد تساقط الأمطار بالخصائص التضاريسية التي تؤدي إلى سرعة تحويل مياه الأمطار إلى مياه جريان سطحي وسيلي وزيادة سرعة التدفق. وسوف تتناول هذه الدراسة تحليل العديد من الخصائص التضاريسية ذات المدلول الجيومورفولوجي والهيدرولوجي التي تسمح بمقارنة أحواض الروافد المغذية لوادي الباطن داخل النطاق العمراني لمدينة حفر الباطن. كما تتناول دراسة العلاقات الارتباطية بين الخصائص التضاريسية. وقد تم الحصول على قيم هذه المتغيرات من مخرجات نموذج الارتفاعات الرقمية من آستر بدقة 30 م باستخدام تطبيقات التحليل المكاني في برنامج ArcGIS.
3-1 الارتفاع الأقصى للحوض:
هو عبارة عن أعلى منسوب على خط تقسيم المياه. ويتراوح الارتفاع الأقصى بين 378 م بالحوض (1) و435 م بالحوضين (8، 7).
3-2 الارتفاع الأدنى للحوض:
هو عبارة عن أدنى منسوب على خط تقسيم المياه ويمثل ارتفاع مصب الحوض المائي. ويتراوح الارتفاع الأدنى بين 310 م بالحوضين (5،10)و 320 م بالحوضين (6، 1).
3-3 الارتفاع المتوسط للحوض المائي:
هو عبارة عن الارتفاع الذي يمثل 50% من ارتفاعات الحوض المائي. وهو يتراوح بين 349 م بالحوض (1)و 377م بالحوض (7).
| الشكل رقم (14) تصنيف أحواض الروافد المدروسة حسب الارتفاع المتوسط |
وتؤثر ارتفاعات التضاريس على نشاط عمليات التعرية وعلى حركة الرواسب الناتجة عنها من المناطق الأكثر ارتفاعاً نحو المناطق المنخفضة تحت تأثير عاملي الجاذبية والانحدار. كما تؤثر الارتفاعات على المدى التضاريسي الذي يمثل الفارق بين أعلى وأدنى ارتفاعين ومن ثم على درجة الانحدار المرتبطة به. وعليه يتراوح الارتفاع المتوسط بأحواض الروافد المدروسة بين 349م بالحوض (1) و377م بالحوض (7). ويمكننا تصنيف أحواض الروافد المدروسة حسب الارتفاع المتوسط إلى ثلاث فئات كما يبينه الشكل رقم (15).
3-4 الطول الأقصى للمجاري:
هو عبارة عن أقصى طول للمجاري الذي تصب في نفس الشبكة المائية. ويؤثر الطول الأقصى للمجاري على زيادة فرص ضياع مياه الجريان السطحي بواسطة عمليتي التبخر والتسرب خلال جريانها من المناطق المرتفعة نحو المناطق المنخفضة، ويتناسب الطول الأقصى للمجاري مع استطالة الحوض المائي ومع زيادة تعرجات المجرى، وعليه يؤثر الطول الأقصى للمجاري على زمني التركيز والاستجابة للحوض المائي، بحيث يرتفع زمن التركيز وزمن الاستجابة مع زيادة الطول الأقصى للمجاري والعكس صحيح. ويبدو أن وادي الحوض (9) يتسم بأطول مجرى وبطول يبلغ 43.87 كم وأن وادي الحوض(1) هو أقل الأودية طولاً وبطول لا يتعدى 4.81 كم. ويتناسب الطول الأقصى للمجاري مع طول الحوض المائي كما يبينه الشكل رقم (5). ويمكننا تصنيف أحواض الروافد المدروسة إلى ثلاث فئات حسب اطوال المجاري المائية كما الشكل رقم (15).
3-5 نسبة الانحدار للحوض المائي:
عرف سرديفي عام 2001 نسبة الانحدار للحوض المائي بالعلاقة النسبية بين فارق الارتفاع بين الارتفاعين الأقصى والأدنى من جهة وطول الحوض المائي من جهة ثانية . وتحسب هذه العلاقة بتطبيق المعادلة الرياضية التالية:
أقصى ارتفاع للحوض (م) أدنى ارتفاع للحوض (م)
نسبة الانحدار
طول الحوض المائي (كم)
ويؤثر انحدار الحوض على طاقة عمليات التعرية بزيادة عملية الحفر الرأسي للمجاري المائية بالمناطق شديدة الانحدار مما يساعد على ارتفاع كميات الرواسب المنقولة بواسطة مياه الجريان السطحي. كما يؤثر انحدار سطح الحوض المائي على سرعة حركة المواد الصخرية الناتجة من عمليات التعرية المائية وعلى المسافة التي تقطعها هذه المواد من أعلي التضاريس نحو المناطق الأقل انحداراً وحتى استقرارها بمناطق الترسيب. كما يرتبط انحدار السطح بطول الحوض المائي وبالمدى التضاريسي له، بحيث يتزايد الانحدار كلما ارتفع المدى التضاريسي وتقلص طول الحوض المائي والعكس صحيح . وتتباين نسبة انحدار الحوض المائي بأحواض الروافد المدروسة بحيث تتراوح بين 3.23 م/كم بالحوض (9)و 13.90 م/كم بالحوض (1). وعليه يمكننا تصنيف أحواض الروافد المدروسة إلى ثلاث فئات حسب نسبة انحدار سطحها الشكل رقم (16) وهي:
الشكل رقم (16) تصنيف أحواض الروافد المدروسة حسب نسبة الانحدار للحوض المائي
3-6 متوسط انحدار أطول مجرى:
هو عبارة عن العلاقة النسبية بين فارق الارتفاع بين الارتفاعين الأقصى والأدنى من جهة وأطول طول للمجاري المائية من جهة ثانية. ويحسب متوسط انحدار أطول مجرى مائي بالحوض بتطبيق المعادلة الرياضية التالية:
أقصى ارتفاع (م) أدنى ارتفاع (م)
متوسط انحدار أطول مجرى
طول أطول مجرى مائي بالحوض (كم)
وتتراوح قيم متوسط انحدار أطول مجرى مائي بالأحواض بين 2.60 م/كم بالحوض (9)و 12.05 م/كم بالحوض (1).
3-7 متوسط انحدار خط تقسيم المياه:
وضع ابلوف 1963 العلاقة النسبية بين الارتفاع الأقصى ومحيط الحوض المائي لحساب متوسط انحدار خط تقسيم المياه بتطبيق المعادلة الرياضية التالية:
2 الارتفاع الأقصى بالحوض المائي (م)
متوسط انحدار خط تقسيم المياه
طول محيط الحوض المائي (كم)
وبتطبيق هذه المعادلة نجد أن متوسط انحدار خط تقسيم المياه للأحواض المدروسة يتراوح بين 7.47 بالحوض (9)و 74.77 م/كم بالحوض (1). ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاثة فئات حسب نسبة انحدار خط تقسيم المياه كما يبينه الشكل رقم (17).
|
الشكل رقم (17) تصنيف أحواض الروافد المدروسة حسب نسبة الانحدار لخط تقسيم المياه |
3-8 التضاريس النسبية:
وضع ميلتون سنة 1957 معادلة لحساب نسبة التضاريس النسبية من العلاقة النسبية بين ارتفاعات الحوض وطول محيطه. ويعبر عنها بتطبيق المعادلة الرياضية التالية:
فارق الارتفاع بين أقصى وأدنى ارتفاعين بالحوض المائي)م)
التضاريس النسبية
طول محيط الحوض المائي (كم)
وبتطبيق هذه المعادلة نجد أن نسبة التضاريس النسبية للأحواض المدروسة تتراوح بين 0.98 م/كم بالحوض (9)و 5.73 م/كم بالحوض (1). ولقد أوضح كل من جريجوري وولينج عام 1973 في دراسة تمت على مجموع 76 حوض مائي بجنوب دايفون ببريطانيا أن التضاريس النسبية تتأثر بمساحة التصريف، بحيث اتضح أن قيمة التضاريس النسبية ترتفع بالأحواض الصغيرة عنها بالأحواض الكبيرة (Gregoy & Walling, 1973 , p. 42) .و لا يختلف الوضع بالنسبة لأحواض الروافد المدروسة. ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاث فئات حسب نسبة التضاريس النسبية كما يبينه الشكل رقم (18).
الشكل رقم (18) تصنيف أحواض الروافد المدروسة حسب نسبة التضاريس النسبية
3-9 نسبة التضاريس:
هي عبارة عن العلاقة النسبية بين ارتفاعات الحوض وطول المجرى الرئيس . ويعبر عن قيمة هذه النسبة بواسطة المعادلة الرياضية التالية:
فارق الارتفاع بين أقصى وأدنى ارتفاعين بالحوض المائي (م)
نسبة التضاريس
طول الحوض (كم)
وبتطبيق هذه المعادلة نجد أن نسبة التضاريس للأحواض المدروسة تتراوح بين 3.23 م/كم بالحوض (9)و 13.90 م/كم بالحوض (1). ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاث فئات حسب نسبة التضاريس كما يبينه الشكل رقم (19).
| الشكل رقم (19): تصنيف أحواض الروافد المدروسة حسب نسبة التضاريس |
3-10 إجمالي تضاريس الحوض:
وضع سترايلر 1952 تعريفا لإجمالي تضاريس اعتماداً على فارق الارتفاع بين أقصى وأدنى ارتفاعين بالحوض المائي (م). ويعبر عن قيمتها بواسطة المعادلة الرياضية أسفله:
إجمالي تضاريس الحوض الارتفاع الأقصى بالحوض المائي بالمتر الارتفاع الأدنى بالمتر
وبتطبيق هذه المعادلة نجد أن اجمالي التضاريس للأحواض المائية المدروسة يتراوح بين 58 م بالحوض (1)و 124 م بالحوض (8). ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاث فئات حسب اجمالي التضاريس كما يبينه الشكل رقم (20) وهي:
الشكل رقم (20): تصنيف أحواض الروافد المدروسة حسب اجمالي التضاريس
3-11 التكامل الهيبسومتري:
قدم كل من بيكو وليسون عام 1971 نموذجا لحساب التكامل الهيبسومتري من العلاقة النسبية بين فارق الارتفاع بين الارتفاعين المتوسط والأدنى من جهة والمدى التضاريسي الذي يعبر عنه بفارق الارتفاع بين الارتفاعين الأقصى والأدنى من جهة ثانية.
ويمكن حساب التكامل الهيبسومتري بتطبيق المعادلة الرياضية التالية:
الارتفاع المتوسط للحوض (م) الارتفاع الأدنى للحوض (م)
التكامل الهيبسومتري
الارتفاع الأقصى للحوض (م) الارتفاع الأدنى للحوض(م)
وبتطبيق هذه المعادلة نجد أن التكامل الهيبسومتري للأحواض المائية المدروسة يتراوح بين 0.40 بالحوضين (5)و (4)و 0.60 بالحوض (6)، أي بمعنى أن الحوضين خمسةو اربعة استكملا 40% من دورة التعرية في حين لم يتبقى للحوض ستة سوى 60% من دورة التعرية . وعليه فإن الحوض ستة يعتبر أكثر الأحواض المائية المدروسة نشاطاً بالنسبة لعمليات التعرية.
ويمكن تصنيف أحواض الروافد المدروسة إلى ثلاث فئات حسب مؤشر التكامل الهيبسومتري كما هو مبين في الشكل رقم (20) وهي:
– العلاقات الارتباطية بين المتغيرات التضاريسية:
تتأثر المتغيرات التضاريسية فيما بينها كما اتضح ذلك من خلال فحص علاقات الارتباط بينها بواسطة ارتباط بيرسون بحيث تبين أن هذه المتغيرات ترتبط فيما بينها بنوعين من علاقات الارتباط هي:
- علاقات ارتباط موجبة وطردية عند مستوى الدلالة 0.01 تربط بين المدى التضاريسي من جهة وطول الحوض وأطول مجرى والارتفاع الأقصى من جهة ثانية. وبين نسبة التضاريس من جهة والتضاريس النسبية وانحدار أطول مجرى وانحدار خط تقسيم المياه وانحدار الحوض من جهة ثانية. وبين التضاريس النسبية من جهة وانحدار أطول مجرى وانحدار خط تقسيم المياه وانحدار الحوض من جهة ثانية. وبين انحدار أطول مجرى من جهة وانحدار خط تقسيم المياه وانحدار الحوض من جهة ثانية. وبين انحدار الحوض من جهة وأطول مجرى والارتفاع الأقصى والارتفاع المتوسط من جهة ثانية. وبين انحدار خط تقسيم المياه من جهة وأطول مجرى والارتفاع الأقصى من جهة ثانية. وبين أطول مجرى وانحدار الحوض. وبين انحدار الحوض من جهة والارتفاع الاقصى والارتفاع المتوسط من جهة ثانية. وبين الارتفاع الأدنى والارتفاع المتوسط.
- هناك علاقات ارتباط عكسية عند مستوى الدلالة 0.01 تربط بين المدى التضاريسي من جهة ونسبة التضاريس والتضاريس النسبية وانحدار أطول مجرى وانحدار الحوض وانحدار خط تقسيم المياه من جهة ثانية. وبين نسبة التضاريس من جهة وطول الحوض ومحيطه وأطول مجرى والارتفاع الأقصى والارتفاع المتوسط من جهة ثانية. وبين التضاريس النسبية من جهة وطول الحوض ومحيطه وأطول مجرى والارتفاعين الأقصى والمتوسط من جهة ثانية. وبين انحدار أطول مجرى من جهة وطول الحوض ومحيطه وأطول مجرى والارتفاعين الأقصى والمتوسط من جهة ثانية. وبين طول الحوض من جهة وانحدار خط تقسيم المياه وانحدار الحوض من جهة ثانية. وبين محيط الحوض من جهة وانحدار خط تقسيم المياه وانحدار الحوض من جهة ثانية. وبين انحدار خط تقسيم المياه من جهة وأطول مجرى والارتفاع الأقصى من جهة ثانية. وبين أطول مجرى وانحدار الحوض. وبين انحدار الحوض والارتفاعين الأقصى والمتوسط.
- ايضا هناك علاقات ارتباط طردية بين المتغيرات التضاريسية عند مستوى الدلالة 0.05 تربط بين المدى التضاريسي من جهة ومحيط الحوض والارتفاع الأقصى من جهة ثانية. وبين الارتفاع المتوسط والتكامل الهيبسومتري.
- في حين هناك علاقة ارتباط واحدة سالبة وذات أهمية احصائية عند مستوى الدلالة 0.05 تربط بين انحدار خط تقسيم المياه والارتفاع المتوسط.
ومن خلال تحليل الخصائص المورفومترية لعشرة أحواض روافد تهدد المناطق العمرانية بمدينة حفر الباطن تبين ان جميع أحواض الروافد المدروسة تتميز بأشكال تختلف عن الشكل الدائري وان الأحواض الأكثر قدرة على تصريف مياه الامطار وتحويلها إلى سيول هي الأحواض (10،5،1)، كما تبين ان الحوض (1) هو اكثر الأحواض المدروسة انحداراً .ومن خلال الفحص الاحصائي لعلاقات الارتباط بين المتغيرات المورفومترية فيما بينها والمتغيرات التضاريسية ظهر نوعين من العلاقات الارتباطية (طرديةو عكسية) عند مستوى الدلالة 0.05 و0.01 .
4- الخصائص الهيدرولوجية لأحواض التصريف:
تعد منطقة حفر الباطن كغيرها من مناطق المملكة العربية السعودية بقلة الأمطار التي تتسم بمتوسطات تساقط سنوية تتراوح بين (50:100 ملم (وفقاً لبيانات محطة القيصومة. ونظراً لوقوع مدينة حفر الباطن على مجرى وادي الباطن وروافد الممتد من شرق المدينة المنورة فان المياه الآتية من السيول ليست قاصرة على منطقة الدراسة وانما تأتي من خارج المنطقة ايضاً.
ومن خلال دراسة عنصر الامطار على منطقة الدراسة نجد انها تتصف بعدم إنتظام تساقطها في الزمان والمكان، وتساقطها على شكل زخات قصيرة وسريعة،و تساقطها بشكل مركز في الزمان ومحدودة في المكان لأنها تنتج في أكثر الأحيان من عواصف محلية.
وتلعب كل هذه الظروف الطبيعية دورًا أساسيًا في سرعة تحويل مياه الأمطار المتساقطة إلى مياه جارية، ونظًرا لعدم توفر محطات هيدرومترية لقياس الجريان السطحي على أودية منطقة الدراسة فإنه تم تطبيق النموذج المقترح من الهيئة الامريكية لحماية التربةSCS . ويقدم هذا النموذج طريقة مناسبة لتقدير تدفق الذروة للسيول إعتمادا على كميات الأمطار السنوية ومساحة التصريف للحوض المائي وزمن التركيز لمساحة التصريف، وقد تم تقدير تدفق الذروة لسيول حوض وادي الباطن وروافده بإستخدام هذا النموذج. لذا سوف تتناول الدراسة في هذه الدراسة نموذج حساب تدفق السيول وتقدير تدفق الذروة والعلاقات الارتباطية بين المتغيرات المورفومترية وتدفق السيول وسرعة الجريان والعلاقات الارتباطية بين المتغيرات التضاريسية وتدفق السيول وسرعة الجريان.
5- تحليل الخصائص الهيدرولوجية لأحواض التصريف:
تعتبر الخصائص الهيدرولوجية محصلة للعلاقات المتبادلة بين الظروف المناخية والخصائص الجيولوجية والتضاريسية لحوض التصريف، وتواجه الدراسات الهيدرولوجية بالمناطق الجافة كثيراً من الصعوبات التي تتعلق بقلة أو بغياب محطات قياس الجريان (المحطات الهيدرومترية) أو قلة البيانات الهيدرولوجية بالمحطات القليلة المتوفرة، ولذا فقد تقدمت الكثير من الدراسات الهيدرولوجية بالعديد من النماذج الرياضية لتقدير جريان السطح وتدفق السيول اعتماداً على الخصائص التضاريسية والمناخية والمورفومترية والجيومورفولوجية لأحواض التصريف كنموذج الهيئة الأمريكية لحماية الأراضي (SCS) الذي يعتبر من أكثر النماذج المستخدمة في تقدير الجريان السطحي بالأحواض المائية التي لا تتوفر بها محطات هيدرومترية على غرار أحواض روافد وادي الباطن لتي تؤثر في جريانها على الكتلة العمرانية الممتدة في مجاريها والمناطق السكنية بالمدينة. ويتيح هذا النموذج تحديد جملة من المتغيرات الهيدرولوجية هي: زمن التركيز للحوض المائيو مدة العاصفة المطرية وفترة الاستجابة للحوض المائيو زمن وصول التدفق للذروةو زمن الأساس للسيلو زمن انخفاض السيلو سرعة الجريان . ولذا تعرض الدراسة تعاريف هذه العناصر كما أوردتها الهيئة الأمريكية لحماية التربة (NRCS,2010) وحساب قيمها بأحواض التصريف المدروسة.وفيما يلي دراستها في منطقة الدراسة:
5-1 زمن التركيز للأحواض المائية:
زمن التركيز للحوض المائي هو المدة الزمنية التي تستغرقها مياه الأمطار في الوصول من أبعد نقطة على خط تقسيم المياه إلى مصب الحوض. وتفيد دراسة زمن التركيز في التعرف على المدة الزمنية الضرورية لوصول مياه الأمطار التي تتحول إلى مياه جارية سطحية وإلى مياه تدفق سيلي تصل من أبعد نقطة في الحوض إلى المصب.
ويتأثر زمن التركيز بكثير من العوامل الطبيعية السائدة بحوض التصريف وخاصة كمية الهطول ونسبة الانحدار ودرجة النفاذية للصخور ومعدلي التسرب والتبخر.
وهناك العديد من النماذج الرياضية التي تعتمد على الخصائص التضاريسية والمورفومترية في تقدير زمن التركيز من أهمها نموذج كيربيش عام 1940 الذي صاغ معادلته بعد دراسته لسبعة أحواض مائية طبيعية في ولاية تينيسي الأمريكية. ويحسب زمن التركيز بهذا النموذج بتطبيق المعادلة الرياضية التالية:
0.06628 × (طول المجرى الرئيس (كم))0.77
زمن التركيز
(متوسط انحدار الحوض المائي م/م)0.385
وبالاعتماد على زمن التركيز لكل حوض مائي يمكننا تصنيف أحواض التصريف المدروسة حسب زمن التركيز إلى ثلاث فئات كما يبينها والشكل رقم (21).
| الشكل رقم (21) تصنيف أحواض الروافد المدروسة حسب زمن التركيز |
5-2 مدة فائض الأمطار:
تعرف الهيئة الأمريكية لحماية التربة مدة فائض الأمطار بالمدة التي يتطلبها الحوض المائي لتحويل مياه الأمطار إلى مياه جريان سطحي أو إلى تدفق سيلي بعد تشبع التربة والمنكشفات الصخرية بالمياه .وتحسب هذه المدة بتطبيق المعادلة الرياضية التالية:
مدة فائض الأمطار 0.133 زمن التركيز للحوض المائي (ساعة) وتتباين مدة فائض الأمطار بأحواض الروافد المدروسة بحيث يمكننا تصنيفها حسب مدة فائض الامطار إلى ثلاث فئات من خلال الشكل رقم (22) .
الشكل رقم (22): تصنيف أحواض الروافد المدروسة حسب مدة فائض الأمطار
5-3 فترة الاستجابة (التباطؤ) للحوض المائي:
وهي المدة الزمنية الضرورية لوصول التسرب إلى أقصاه وبداية تحول كميات الأمطار إلى تدفق سطحي. ولذا فإن نوعية التربة ونسبة الانحدار ودرجة النفاذية تتحكم بشكل كبير في تحديد فترة الاستجابة. وتحسب هذه الفترة بتطبيق المعادلة الرياضية التالية:
فترة الاستجابة (التباطؤ) 0.6 زمن التركيز للحوض المائي (ساعة)وتتباين فترة الاستجابة بأحواض الروافد المدروسة بحيث يمكننا تصنيفها إلى ثلاث فئات حسب فترة الاستجابة كما يبينه الشكل رقم (23) وهي:
| الشكل رقم (23): تصنيف أحواض الروافد المدروسة حسب فترة الاستجابة
|
5-4 مدة وصول التدفق للذروة:
وهي المدة الزمنية الفاصلة بين بداية الجريان السطحي بالحوض ووصول التدفق للذروة.
وتحسب هذه المدة بتطبيق المعادلة الرياضية التالية:
مدة وصول التدفق للذروة ½ مدة فائض الأمطار (ساعة) فترة الاستجابة للحوض المائي (ساعة) وترتبط مدة وصول التدفق للذروة بشكل مباشر مع فترة استجابة الحوض كما يبينه بيانات الملحق رقم 6 . ويتطابق تصنيف أحواض التصريف المدروسة حسب مدة وصول التدفق للذروة مع فترة الاستجابة للحوض المائي.
5-5 فترة الأساس للسيل:
وهي الفترة الزمنية من بداية جريان السيل حتى عودة المياه الجارية السطحية إلى مستواها الطبيعي، وهي تحسب بتطبيق المعادلة الرياضية التالية:
فترة الأساس للسيل 2.67 مدة وصول التدفق للذروة (ساعة) ونجد أن مساحة التصريف للحوض المائي تفسر بنسبة 94% تباينات فترة الأساس للسيل بأحواض الروافد المدروسة. كما يتطابق التوزيع المكاني لتباينات فترة الأساس للسيل مع التوزيع المكاني لفترة استجابة الحوض ولمدة وصول التدفق للذروة . ويمكن تصنيف أحواض الروافد المدروسة حسب فترة الأساس للسيل إلى ثلاث فئات كما يبينه الشكل رقم (24) وهي:
| الشكل رقم (24): تصنيف أحواض الروافد المدروسة حسب فترة الأساس للسيل
|
5-6 فترة انخفاض تدفق السيل:
وهي الفترة الزمنية التي تفصل بين تدفق الذروة ومستوى الجريان الطبيعي. وتحسب هذه الفترة بتطبيق المعادلة الرياضية التالية:
فترة انخفاض تدفق السيل 1.67 مدة وصول التدفق للذروة (ساعة) وتتأثر فترة انخفاض تدفق السيل بفترة الأساس للسيل وهي ترتبط بشكل كبير أيضاً بمساحة التصريف للحوض المائي بحيث نجد أن تصنيف أحواض الروافد حسب فترة انخفاض تدفق السيل يتطابق تماماً مع تصنيفها حسب فترة الأساس للسيل كما يبينه.
5-7 سرعة الجريان (التدفق):
تعد سرعة الجريان من أهم المعاملات الهيدرولوجية لحوض التصريف لأنها هي التي تؤدي إلى حدوث الخسائر المادية والبشرية أثناء حدوث السيول. ونظراً لصعوبة قياس سرعة الجريان أو التدفق بالأحواض المائية التي لا تتوفر على محطات هيدرومترية مثل الأحواض المدروسة فإنه يمكن حساب هذه السرعة بتطبيق المعادلة الأساسية لحساب السرعة وهي النسبة بين المسافة والزمن(أبو العينين، 2007). بحيث تمثل المسافة طول الحوض المائي (كم) والزمن هو زمن التركيز للحوض المائي (ساعة). وعليه فإن سرعة الجريان تساوي:
طول الحوض المائي (كم)
سرعة الجريان
زمن التركيز للحوض المائي (ساعة)
وبالاعتماد على سرعة الجريان بكل حوض مائي يمكننا تصنيف أحواض التصريف المدروسة حسب سرعة الجريان السطحي إلى ثلاث فئات كما هو موضح بالشكل (25) الآتي:
| الشكل رقم (25) تصنيف أحواض الروافد المدروسة حسب سرعة الجريان
|
5-8 تدفق الذروة:
ينتج تدفق الذروة من كمية الجريان السطحي التي تحدث من فائض الأمطار بكميات تفوق كميات التسرب والتبخر. وتحسب كمية التدفق من نموذج الهيئة الأمريكية لحماية التربة بتطبيق المعادلة الرياضية التالية:
تقدير تدفق الذروة 2.8 (كمية فائض الامطار او الجريان السطحي خلال مدة العاصفة المطرية (ملم) مساحة الحوض المائي (كم2) مدة وصول التدفق للذروة (ساعة))
ولحساب تدفق الذروة للسيول يجب حساب فائض الأمطار باستخدام معامل الجريان السطحي وبتطبيق المعادلة التالية:
فائض الامطار ملم/ يوم معامل الجريان السطحي كمية الأمطار (ملم) معامل الجريان السطحي وهو يستخرج من جدول خاص (الملحق رقم 5) .ومن خلال بيانات معامل الجريان السطحي لأنواع الأراضي فقد تم اعتماد متوسط معامل الجريان الذي يتراوح بين 0.30و 0.10 المناسب لأحواض التصريف الطبيعية التي لا تحتوي على محطات قياس الجريان السطحي للأودية كما هو الحال بالنسبة لحوض وادي الباطن . وبالاعتماد على قيم تدفق الذروة للسيول بكل حوض مائي يمكننا تصنيف أحواض التصريف المدروسة إلى ثلاث فئات كما يبينه الشكل رقم (26) وهي على النحو التالي:
| الشكل رقم (26): تصنيف أحواض الروافد المدروسة حسب تدفق الذروة للسيول
|
– العلاقات بين المتغيرات المورفومترية وتدفق السيول وسرعة الجريان:
تؤثر مختلف المتغيرات المورفومترية على زمن التركيز والتدفق وسرعة الجريان السيلي بأحواض الروافد المدروسة بدرجات متفاوتة كما توضحه نتائج فحص ارتباط بيرسون التي يلخصها الجدول رقم (1)، بحيث نجد أن:
- قيمة علاقة الارتباط طردية بين تدفق الذروة للسيول من جهة ومعامل الانبعاج ومساحة التصريف وزمن التركيز من جهة ثانية وهي بلغت على التوالي 0.821و 0.838و 0.956 عند مستوى الدلالة 0.01 بينما نجد أن علاقة الارتباط عكسية بين تدفق الذروة للسيول ومعامل الاندماج
الجدول رقم (1) جدول علاقات الارتباط بين المتغيرات المورفومترية والتدفق وسرعة الجريان السيلي بأحواض الروافد المدروسة
| زمن التركيز | سرعة الجريان | التدفق | المتغير |
| ساعة | متر/ثانية | متر3/ثانية | |
| —– | —– | 0.821** | معامل الانبعاج |
| 0.762-** | —– | 0.854-** | معامل الاندماج |
| 0.844** | —– | —– | نسبة الاستدارة |
| 0.840-** | —– | —– | نسبة الاستطالة |
| —– | 0.977-** | —– | معامل الشكل |
| —– | 0.758-** | —– | طول الحوض |
| 0.980** | —– | 0.750.** | محيط الحوض |
| 0.972** | —– | 0.838** | مساحة الحوض |
| —– | —– | 0.956** | زمن التركيز ساعة |
*مستوى الأهمية: 0.05 **مستوى الأهمية: 0.01
وقد بلغت 0.854- عند مستوى الدلالة 0.01.
- قيمة علاقة الارتباط عكسية بين سرعة الجريان ومعامل الشكل بما يعادل 0.799- عند مستوى الدلالة 0.01 وبين سرعة الجريان وطول الحوض بما يعادل 0.758- عند مستوى الدلالة 0.05.
- قيمة علاقة الارتباط طردية بين زمن التركيز من جهة ونسبة الاستدارة ومحيط الحوض ومساحته من جهة ثانية، بحيث بلغت على التوالي 0.844و 0.980و 0.972 عند مستوى الدلالة 0.01.
- قيمة علاقة الارتباط عكسية بما يعادل 0.762- بين معامل الاندماج وزمن التركيز عند مستوى الدلالة 0.01 وبما يعادل 0.840- بين زمن التركيز ونسبة الاستطالة عند مستوى الدلالة 0.05.
– العلاقات بين المتغيرات التضاريسية وتدفق السيول وسرعة الجريان:
تؤثر المتغيرات التضاريسية على زمن التركيز والتدفق وسرعة الجريان السيلي بأحواض الروافد المدروسة بدرجات متفاوتة كما توضحه نتائج فحص ارتباط بيرسون التي يلخصها الجدول رقم (2) وهي:
| الجدول رقم (2) مصفوفة علاقات الارتباط بين المتغيرات التضاريسية والتدفق وسرعة الجريان السيلي بأحواض الروافد المدروسة
|
| زمن التركيز
ساعة |
سرعة الجريان
متر/ثانية |
التدفق
متر3/ثانية |
المتغير |
| —– | —– | 0.821** | زمن التركيز ساعة |
| 0.830** | —– | 0.823** | اجمالي التضاريس |
| 0.916-** | 0.663* | 0.745-** | نسبة التضاريس |
| 0.939-** | —– | 0.851-** | التضاريس النسبية |
| 0.892-** | —– | 0.723-** | انحدار أطول مجرى |
| 0.990** | —– | 0.753** | طول أطول مجرى |
| 0.916-** | 0.663-* | 0.745-** | انحدار الحوض |
| 0.825** | 0.702* | 0.645* | الارتفاع المتوسط |
*مستوى الأهمية: 0.05 **مستوى الأهمية: 0.01
- هناك علاقة ارتباط طردية بين تدفق الذروة للسيول من جهة وزمن التركيز واجمالي التضاريس من جهة ثانية وهي بلغت على التوالي 0.821 و0.823 عند مستوى الدلالة 0.01 .بينما نجد أن هناك علاقة ارتباط عكسية بين تدفق الذروة للسيول والتضاريس النسبية وقد بلغت 0.851- عند مستوى الدلالة 0.01.
- كما توجد علاقة ارتباط طردية بين تدفق الذروة للسيول من جهة وطول أطول المجاري والارتفاع المتوسط من جهة ثانية وهي بلغت على التوالي 0.753و 0.645 عند مستوى الدلالة 0.05 . بينما نجد علاقة ارتباط عكسية بين تدفق الذروة للسيول من جهة ونسبة التضاريس وانحدار أطول مجرى وانحدار الحوض من جهة ثانية وقد بلغت على التوالي 0.745-و 0.723-و 0.745- عند مستوى الدلالة 0.05.
- علاقة ارتباط عكسية بين نسبة التضاريس وانحدار الحوض من جهة وسرعة الجريان من جهة ثانية وبما يعادل 0.663- عند مستوى الدلالة 0.05 . بينما توجد علاقة ارتباط طردية بين سرعة الجريان والارتفاع المتوسط بما يعادل 0.702 عند مستوى الدلالة 0.05.
- علاقة ارتباط طردية بين زمن التركيز من جهة واجمالي التضاريس وطول أطول مجرى والارتفاع المتوسط من جهة ثانية بحيث بلغت على التوالي 0.830 و0.990و 0.825 عند مستوى الدلالة 0.01.
- علاقة ارتباط عكسية بين زمن التركيز من جهة ونسبة التضاريس والتضاريس النسبية وانحدار أطول مجرى وانحدار الحوض من جهة ثانية بما يعادل على التوالي 0.919-و 0.939-و 0. 892- و0.916- عند مستوى الدلالة 0.01.
الخلاصة
توصلت الدراسة إلى تحديد 10 أحواض مائية لأودية رافدة لوادي الباطن لها تأثيرات على امتداد المساحة العمرانية لمدينة حفر الباطن منها 4 أحواض تقل مساحاتها عن 20 كم2و 4 أحواض تتراوح مساحاتها بين 20و 100 كم2 وحوضين آخرين تفوق مساحاتهما 100 كم2. وقد تم استخدام علاقة الارتباط لبيرسون التي أظهرت العلاقات التالية:
- علاقات ارتباط طردية (موجبة) عند مستوى الدلالة 0.01 بين 8 متغيرات مورفومترية هي نسبة الاستطالة ومعامل الشكل وعلاقة الطول بالمساحة ومتوسط عرض الحوض والمحيط النسبي وطول الحوض ومحيطه ومساحته.
- علاقات ارتباط عكسية عند مستوى الدلالة 0.01 بين 7 متغيرات مورفومترية هي نسبة الطول إلى العض ونسبة الاستطالة ومعامل الشكل ومعامل الانبعاج وعلاقة الطول بالمساحة ومتوسط عرض الحوض والمحيط النسبي.
- علاقات ارتباط طردية (موجبة) عند مستوى الدلالة 0.05 بين 6 متغيرات مورفومترية هي معامل الاندماج ونسبة الطول إلى العرض ومساحة الحوض والمحيط النسبي وطول الحوض ومحيطه.
- علاقات ارتباط عكسية عند مستوى الدلالة 0.05 بين 6 متغيرات مورفومترية هي معامل الانبعاج وطول الحوض ومساحته ومحيطه ونسبة الاستدارة ونسبة الطول إلى المساحة.
- كما تم تحديد الخصائص التضاريسية من خلال حساب 11 متغير تضاريسي للأحواض المدروسة وقد تبين من خلال تحليل الخصائص التضاريسية أن الأحواض المدروسة استكملت ما بين 40: 60% من دورة التعرية.
- ولتحليل العلاقة بين المتغيرات التضاريسية تم استخدام علاقة الارتباط لبيرسون التي أظهرت أن هناك:
- علاقات ارتباط طردية (موجبة) عند مستوى الدلالة 0.01 بين 11 متغير تضاريسي هي المدى التضاريسي وطول الحوض وأطول مجرى والارتفاع الأقصى ونسبة التضاريس والتضاريس النسبية وانحدار خط تقسيم المياه وانحدار الحوض والارتفاع المتوسط والارتفاع الأدنىأطول مجرى وانحدار خط تقشسيم المياه خط .
- علاقات ارتباط عكسية عند مستوى الدلالة 0.01 بين 10 متغيرات تضاريسية هي المدى التضاريسي وطول الحوض وانحدار أطول مجرى والارتفاع الأقصى ونسبة التضاريس والتضاريس النسبية وانحدار خط تقسيم المياه وانحدار الحوض والارتفاع المتوسط ومحيط الحوض.
- علاقات ارتباط طردية (موجبة) عند مستوى الدلالة 0.05 بين 5 متغيرات تضاريسية هي المدى التضاريسي والارتفاع الأقصى والارتفاع المتوسط ومحيط الحوض والتكامل الهيبسومتري.
- علاقة ارتباط واحدة سالبة ذات أهمية احصائية عند مستوى الدلالة 0.05 بين انحدار خط تقسيم المياه والارتفاع المتوسط للحوض.
وتوصلت كذلك هذه الدراسة إلى حساب تدفق الذروة لسيول الأودية المدروسة بتطبيق نموذج SCS Dimensionless Unit Hydrograph باستخدام المتغيرات المورفومترية ومتوسط كميات الأمطار السنوية الذي بلغ 22.3 ملم/يوم بمحطة القيصومة خلال الفترة 1966-2005م، بحيث تم تحديد المتغيرات التالية:
- زمن التركيز بتطبيق نموذج كيربيش، بحيث تراوحت قيم هذا المتغير بين 2.46 ساعة بالحوض (1)و 14.86 ساعة بالحوض (9).وتبلغ مدة فائض الأمطار بين 0.33 ساعة بالحوض (1)و 1.98 ساعة بالحوض (9). وتبلغ فترة استجابة الحوض، التي تراوحت قيم هذا المتغير بين 1.48 ساعة بالحوض (1)و 8.92 ساعة بالحوض (9).و تبلغ مدة وصول التدفق للذروة، التي تراوحت قيم هذا المتغير بين 1.64 ساعة بالحوض (1)و 9.90 ساعة بالحوض (9).
وتبلغ فترة الأساس للسيول، التي تراوحت قيم هذا المتغير بين 4.38 ساعة بالحوض (1)و 26.44 ساعة بالحوض (9). وتبلغ فترة انخفاض السيل، التي تراوحت قيم هذا المتغير بين 2.74 ساعة بالحوض (1)و 16.54 ساعة بالحوض (9).وتبلغ سرعة الجريان، التي تراوحت قيم هذا المتغير بين 1.50 م/ثانية بالحوضين (2)و (5)و 2.37 ساعة بالحوض (9).وتبلغ كمية فائض الأمطار 4.5 ملم/يوم. وتبلغ متوسط تدفق الذروة للسيول المناسب لمتوسط الأمطار السنوي بمحطة القيصومة، بحيث تراوحت قيم هذا المتغير بين 30.04 م3/ثانية بالحوض (1) و257.58 م3/ثانية بالحوض (10).
ولقد أظهر تحليل العلاقة بين المتغيرات المورفومترية من جهة وتدفق الذروة للسيول وسرعة الجريان من جهة ثانية عدة علاقات ارتباط هامة هي:
- علاقات ارتباط طردية (موجبة) عند مستوى الدلالة 0.01 بين تدفق الذروة للسيول من جهة و 3 متغيرات هي معامل الانبعاج ومساحة التصريف وزمن التركيز أطول مجرى وانحدار خط تقسيم المياه خط . وعلاقة ارتباط عكسية بين سرعة الجريان من جهة ومتغيران هما معامل الشكل وطول الحوض من جهة ثانية عند مستوى الدلالة 0.01و 0.05 على التوالي. وعلاقات ارتباط طردية (موجبة) عند مستوى الدلالة 0.01 بين زمن التركيز من جهة ونسبة الاستدارة ومحيط الحوض ومساحته من جهة ثانية. وعلاقة ارتباط عكسية بين زمن التركيز من جهة ومعامل الانبعاج ونسبة الاستطالة من جهة ثانية عند مستوى الدلالة 0.01و 0.05 على التوالي.
وأظهر كذلك تحليل العلاقة بين المتغيرات التضاريسية من جهة وتدفق الذروة للسيول وسرعة الجريان من جهة ثانية عدة علاقات ارتباط هامة هي:
- علاقات ارتباط طردية (موجبة) بين زمن التركيز وإجمالي التضاريس من جهة وبين تدفق الذروة للسيول والتضاريس النسبية من جهة ثانية عند مستوى الدلالة 0.01 أطول مجرى وانحدار خط تقشسيم المياه خط .وعلاقة ارتباط طردية (موجبة) بين تدفق الذروة للسيول من جهة وأطول مجرى والارتفاع المتوسط من جهة ثانية وعلاقة ارتباط عكسية بين تدفق الذروة للسيول من جهة ونسبة التضاريس وانحدار أطول مجرى وانحدار الحوض من جهة ثانية عند مستوى الدلالة 0.05.و علاقات ارتباط طردية (موجبة) عند مستوى الدلالة 0.01 بين زمن التركيز من جهة ونسبة الاستدارة ومحيط الحوض ومساحته من جهة ثانية.
- علاقة ارتباط عكسية بين زمن التركيز من جهة ومعامل الانبعاج ونسبة الاستطالة من جهة ثانية عند مستوى الدلالة 0.01و 0.05 على التوالي. وعلاقة ارتباط عكسية بين سرعة الجريان من جهة ونسبة التضاريس وانحدار الحوض من جهة ثانية وعلاقة طردية بين سرعة الجريان والارتفاع المتوسط عند مستوى الدلالة 0.05.
المراجع العربية:
- ابو العينين، محمود (2007م). جغرافية الموارد المائية مع التطبيق على موارد المياه بالوطن العربي، مكتبة المتنبئ الدمام.
- جاد، طه محمد، (1980) . بعض خصائص التصريف المائي بمرتفعات مصر الشرقية، مجلة معهد البحوث والدراسات العربية، العدد 10، القاهرة، ص ص 269-305.
- جودة، حسنين،و آخرون (١٩٩١) . وسائل التحليل الجيومورفولوجى، الطبعة الأولى، القاهرة.
- صالح، احمد (1989). الجريان السيلي في الصحارى – دراسة في جيومرفولوجية الاودية الصحراوية، معهد البحوث والدراسات العربية، العدد 51، القاهرة.
- عزيز، مكي (1972). الامطار في المملكة العربية السعودية، جامعة الرياض، مجلة كلية الآداب، م2، الرياض .
- كليو، عبد الحميد (١٩٨٨). أودية حافة جبال الـزور بالكويـت تحليـل جيومورفولـوجي، الجمعية الجغرافية الكويتية، الكويت.
- هيئة المساحة الجيولوجية السعودية (2012). حقائق وأرقام، جدة.
المراجع الاجنبية:
- Chorley, R. (1957). Illustrating the Laws of Morphometry. Geological Magazine, 94(2),pp 140-150.
- Schumm, S.A. (1954): The relation of drainage basin-relief to sediment loss, Assoc. Int. Sci. Hydrol., Proc. Ass. Gen. Rome, vol 1(36),pp216-219.
- Schumm, S.A. (1956): Evolution of drainage system and slope in badlands of Perth Amboy, New Jersey. Bull. Geol. Soc. Am. Vol. 67,pp216-219.
- O; Sarangi. A and Shamara. M. C. (2008): Hypsometric integral estimation methods and its relevance on erosion status of North-West Lasser Himalaya watersheds, Water Resource Management. No 22,pp1545-1560.
- Zăvoinau I. (1978): Morphometry of hydrographic basins, Ed. Academiei Bucarest.
- Saud, M. (2009), Watershed Characterization of Wadi Aurnah, Western Arabian Peninsula, J. Water Resource and Protection,no 1.
- Schumm, S.A., 1977. The Fluvial System. Wiley, New York.
- Gregory, K.J. and Walling, D.E. (1973) Drainage Basin. Form and Process: A Geomorphological Approach. Edward Arnold, London.
- Horton, R.E.(1945). Erosional development of streams and their drainage basins: Hydrophysical approach to Quantitative morphology. Bull. Geol. Soc. Am. Vol. 56.
- .Kirpich, Z.P. (1940): Time of concentration of small agricultural watersheds, Civil Engineering 10 (6), ASCE, New York,p362..
- De Brouwer, J.A.M. (1997): Determination of Peak runoff , The Integrated Land and Water Information System (ILWIS) Department, Applications Guide, Institute for Aerospace Survey and Earth Sciences, Enschede, The Netherlands , pp. 131-138.
- Arnous, M., and Green, D. (2011). GIS and Remote Sensing as Tools for Conducting Geo-hazards Risk Assessment along Gulf of Aqaba Coastal Zone, Egypt. Springer Science & Business Media. Journal of Coastal Conservation.
- Bishaw, K. (2012). Application of GIS and Remote Sensing Techniques for Flood Hazard and RiskAssessment: The Case of Dugeda Bora Woreda of Oromiya Regional State, Ethiopia.Paper for the 2012 Berlin Conference on the Human Dimensions of Global Environmental Change. Lecturer at Ethiopian Civil Service University. Addis Ababa, Ethiopia.
- Sanyal, J. (2004). Application of GIS and Remote Sensing In Flood Management: A Case Study of West Bengal, India, Department Of Geography, National University of Singapore.
- Gregory, K.J. & Walling, D.E (1973): Drainage basin Form and Process: A Geomorphological Approach , Edward Arnold (Publisher Ltd) , London.
- Abu Elenen , M. (1988): Geological and Geochemical studies on granit rocks of wadi Seih area (West Sinaï), Mansourah University, Egypt.
- National Resources Conservation Service – NRCS (2010): Time of concentration, Chapter 15, Part 630 Hydrology National Engineering Handbook, Department of Agriculture, USA.
- . Hack, J. T. (1957): Studies of longitudinal stream profiles in Virginia and Maryland: U. S. geological survey professional paper, 294-B,pp 45-97.
- Horton, R.E. (1932): Drainage basin characteristics, Trans. Amer. Geophysics. Union, 13,pp 350-361
- Miller, V.C. (1953): A quantitative geomorphic study of drainage basin characteristic in the clinch, Mountain area, Virginia and Tennessee, ProJet NR Tech. Rept.3 Columbia University, Department of Geology, ONR, Geography branch, New York,pp389-342.
- .N.I.H (National Institute of Hydrology) (1999): Geomorphological Study of Devak Basin, CS/AR 33/1998-99, Roorkee 247-667, Jal Vigyan Bhawan, India.
- .Pareta, K and Pareta, U. (2011): Quantitative morphometric analysis of watershed of Yamuna basin (India) using ASTER (DEM) and GIS, International Journal of Geomatics and Geosciences, Vol 2, No 1,pp248-269.
Analysis of morphometric data for drainage basins in Hafr Al Batin city,
northeast of Saudi Arabia using GIS