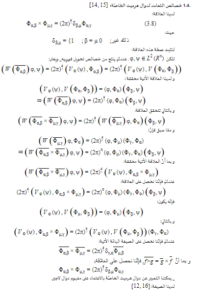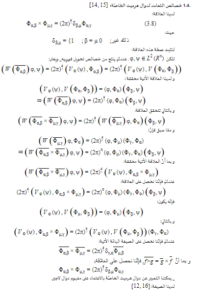Hermite functions and special Hermite functions
depending on Heisenberg group
Soha Ali Salamah
Faculty of Sciences || Al-Baath University || Syria
DOI PDF
Tab title
In this paper we talk about Heisenberg group, the most know example from the lie groups. After that we talk about the representation theory of this group, and the relationship between the representation theory of the Heisenberg group and the position and momentum operator and momentum operators.ors. ielationship b etween the representation theory of the Heisenberg group and the position and momen, that shows how we will make the connection between the Heisenberg group and physics. Then we introduce and study some properties of the Hermite and special Hermite functions. These functions are eigenfunctions of the Hermite and special Hermite operators, respectively. The Hermite operator is often called the harmonic oscillator and the special Hermite operator is sometimes called the twisted Laplacian. As we will later see, the two operators are directly related to the sublaplacian on the Heisenberg group. The theory of Hermite and special Hermite expansions is intimately connected to the harmonic analysis on the Heisenberg group. They play an important role in our understanding of several problems on Hn. Keywords: Heisenberg group, The Schrodinger Representations, Fourier_ Wigner transform, Hermite Functions, Special Hermite Functions .
دوال هرميت ودوال هرميت الخاصة اعتماداً على زمرة هايزنبرغ
سهى علي سلامة
كلية العلوم || جامعة البعث || سوريا
Tab title
الملّخص: عرّفنا في بحثنا هذا زمرة هايزنبرغ، وهي الزمرة الأكثر شهرةً من زمر لي. ثمّ ناقشنا نظريّة التمثيل لهذه الزمرة، إضافةً إلى العلاقة بين نظريّة التمثيل لزمرة هايزنبرغ، ومؤثرات كميّة الحركة والموضع. وهذا ما يُبيّن لنا كيفية تحقيق الترابط بين زمرة هايزنبرغ والفيزياء. ثمَ درسنا خصائص دوال هرميت، ودوال هرميت الخاصّة. إنّ هذه الدوال هي دوال ذاتيّة لمؤثرات هرميت، ومؤثرات هرميت الخاصّة على التوالي. يُطلق عادةً على مؤثر هرميت اسم الهزّاز التوافقي Harmonic oscillation, ويُطلق على مؤثر هرميت الخاص اسم مؤثر لابلاس الملتوي twisted Laplacian. ويرتبط كلٌ من هذين المؤثرَين بمؤثر لابلاس الجزئي على زمرة هايزنبرغ. هذا وإنّ نظريّة مناشير هرميت، ومناشير هرميت الخاصّة ترتبط ارتباطاً وثيقاً بالتحليل التوافقي لزمرة هايزنبرغ Hn، كما أنّها تلعب دوراً هامّاً في فهمنا للعديد من المسائل في Hn. الكلمات المفتاحيّة: زمرة هايزنبرغ، تمثيلات شرودنجر، تحويل فورييه_ ويغنر، دوال هرميت، دوال هرميت الخاصة.
المقدّمة:
يرتبط الإطار الرياضي لميكانيكا الكم Quantum Mechanics ارتباطاً وثيقاً بما يصفه علماء الرياضيات بنظريّة تمثيل الزمر. وفي بحثنا هذا سندرس هذه الفكرة ببعض التفصيل, ونعمل من خلال بعض الأنواع من الزمر, وذلك كنتيجةٍ للعلاقة الأساسيّة بين ميكانيكا الكم ونظرية التمثيل, والتي ببساطة تدور حول أنّه عندما يكون لدينا جملة كموميّة فيزيائيّة تؤثر عليها زمرة G, فإنّ فضاء الحالة لهذه الجملة سيكون كما التمثيل الواحدي للزمرة المؤثرة عليها. وهذا يعني أنّ نظرية التمثيل تُقدّم معلوماتٍ مهمّةً حول فضاءات الحالة الميكانيكية الكموميّة عندما تؤثر زمرة ما على هذه الجملة الفيزيائية. 4,13,16
وبذلك تصبح الفيزياء بالنسبة لعلماء الرياضيات مصدراً مثمراً للغاية لدراسة التمثيلات الواحدية.
كانت بداية ظهور بنية زمر لي عندما لاحظ عالم الرياضيات Sophus Lie عام 1870 العلاقة الوثيقة بين هذا النوع من الزمر, وحلول بعض المعادلات التفاضليّة. ثمّ تمّت الملاحظة بأنّ الموّلدات لزمر لي المؤثرة على فضاءاتٍ مناسبة, لها الصيغة نفسها التي تتميز بها الدوال الخاصّة.
ومن الأمثلة عن زمر لي عديمة القوى نجد زمرة هايزنبرغ, وإنّ موضوع دراستنا في هذا البحث هو أحد التطبيقات على زمرة هايزنبرغ وهي دوال هرميت ودوال هرميت الخاصة.