غدير أحمد سهلي

إدارة تعليم حائل || وزارة التعليم || المملكة العربية السعودية

DOI PDF

أولا: خلفية الدراسة

مقدمة

تولى مسألة الحركة الدورانية الفراغية لجسم متماسك حول نقطة ثابتة اهتماماً كبيراً في الميكانيكا النظرية سواء كان في مجال الجذب النيوتوني أو كان تحت تأثير مجال الجاذبية المتماثل أو في المجال المغناطيسي. وتعزى هذه الأهمية لضرورة حل معادلات تفاضلية غير خطية عددها ستة ولها ثلاثة تكاملات أولية، والتي تكون كمجموعة مغلقة ويتطلب حلها الحصول على ستة تكاملات أولية كما يتطلب حلها أيضا حل مجموعة أخرى من المعادلات التفاضلية من الرتبة الأولى يكون فيها عدد التكاملات الأولية مساوٍ لعدد المعادلات. وعليه، فإن حل هذه المسألة في صورتها العامة قد يكون مستحيلاً في بادئ الأمر ولكن يسهل حلها بطريقة تدريجية باستخدام النظريات المختلفة حول المعادلات التفاضلية. وباستخدام هذه النظريات، يمكن تخفيض عدد التكاملات الأولية اللازمة للحل لتصبح خمسة تكاملات أولية من خلال وضع المعادلات الستة في شكل ست متساويات. كما يمكن تخفيض عدد التكاملات اللازمة للحل إلى أربعة تكاملات أولية فقط من خلال تطبيق نظرية جاكوبي للعامل المتكامل الأخير – وهو معلوم للجسم المتماسك  (Awrejcewicz, & Koruba, 2012)

وعموماً يمكن الحصول على ثلاثة تكاملات أولية للمسألة تسمى (تكامل الطاقة – تكامل كمية الحركة – التكامل الهندسي) (Leimanis، 2013) ويلزم لحل المسألة الوصول إلى حل كامل للحصول على التكامل الأولي الرابع، وهنا تجدر الإشارة إلى عدم إمكانية الحصول على هذا التكامل حتى لحظة كتابة هذا البحث على الرغم من المحاولات والجهود المستمرة من قبل العلماء للوصول إليه خلال القرنين الأخيرين.

وفيما يلي توضيح لتوجه العلماء نحو بحث الحالات الخاصة المختلفة والتي يمكن من خلالها إيجاد التكامل الأولي الرابع:

أولاً: في مجال الجذب المتماثل:

• حالة أويلر – بوانسه ((Yehia, 2015
• حالة لاجرانج – بواسون (Akulenko et al., 2016)
• حالة كوفاليفسكايا (Cooke, 2012)

ثانياً: في مجال الجذب النيوتوني ( توجد حالتين مشابهتين للحالتين التاليتين ):

• ‌أ- حالة أويلر
• ‌ب- حالة لاجرانج

في حالات أخرى، أظهرت البحوث ذات الصلة استحالة وجود تكامل أولي رابع، وبالتالي يستحيل الوصول إلى حلول تحليلية لغير الحالات المذكورة، ولهذا ارتأى الباحث إلى أهمية البحث في كيفية حل الحالات الأخرى المتعلقة بهذه المسألة.

وتوصل الباحثين  (Chae, 2015) و(Odintsov & Oikonomou, 2016)إلى إمكانية تصنيف هذه المسألة إلى عدد كبير من الحالات الخاصة التي يمكن الوصول إليها من المسألة العامة في ظل وجود فيود معينة إما على مركز كتلة الجسم أو على قيم مركبات السرعة الزاوية الابتدائية أو على الاثنين معاً. ومع التقدم في مجالات المعادلات التفاضلية، أدى هذا التصنيف للحصول على حلول دورية على هيئة متسلسلات من القوى تحتوي على بارامتر صغير أمكن تحديد في جميع الحالات وتعتبر (طريقة البارامتر الصغير لبوانكريه) من أهم الطرق التي تعطي الحلول في تلك الحالة، وهي من الطرق الاضطرابية الأكثر شيوعاً والتي من إبداعات الرياضيين والفيزيائيين من حيث إيجاد الحلول التقريبية للمسائل التي يستحيل إيجاد الحل التام لها (Amer، 2008).

وفي ضوء ما ذكر أعلاه، تتناول الدراسة الحالية الحركات المغزلية السريعة لجسم متماسك في مجال قوة نيوتوني.

مشكلة الدراسة

نظراً لأهمية حركة الجيروسكوبات وتطبيقاتها في المجالات المدنية والعسكرية – فهي تستخدم في الرادارات والطائرات والغواصات البحرية وغيرها من المركبات الحديثة – ولهذا فقد استحوذت هذه الحركة باهتمام كثير من المتخصصين في الميكانيكا الكلاسيكية.

وتتميز هذه الحركة بإمكانية وضع قيد مقبول على المعادلات الحاكمة للحركة على صورة فرض قيمة كبيره بدرجة كافية لمركبة السرعة الزاوية حول محور تماثل الجيرسكوب. وتتمثل أهمية هذا القيد في إمكانية اختزال منظومة المعادلات التفاضلية غير الخطية الست من الرتبة الأولى والتكاملات الأولية الثلاث إلى منظومة من معادلتين تفاضليتين شبه خطيتين من الرتبة الثانية وتكامل أولي واحد فقط.

على الرغم من ذلك، تفتقر المكتبة العربية إلى الدراسات المختصة بهذا المجال، ومن هنا تأتي الحاجة إلى ضرورة دراسة حركة الجيروسكوبات وخاصة الحركات الاضطرابية لجيروسكوب متماثل دائر.

أهداف الدراسة

تهدف الدراسة الحالية إلى تحقيق التالي:

1. تفصيل الحركات المغزلية السريعة لجسم متماسك في مجال قوة نيوتوني من ناحية فيزيائية بما يسمح بتوظيفها بشكل افضل في التطبيقات الهندسية والديناميكية.
2. تقديم حلول للحالات الشاذة التي ذكرت في الدراسات السابقة وتوضيحها لما يخدم الاهداف النظرية والتطبيقية.
3. توضيح كيفية استنتاج جيروسكوب لاجرانج كحالة خاصة جداً من الحلول التي حصلنا عليها.

مصطلحات الدراسة

الحركات المغزلية: خاصية تعبر عن دوران الجسيم الأولي حول نفسه. يعتبر اللف المغزلي خاصية جوهرية في كافة الجسيمات الأولية وتمثل ظاهرة ميكانيكية كمومية أصيلة. يمكن تقريب اللف المغزلي للإلكترون للأذهان عن طريق تشبيهها بدوران الأرض حول نفسها إضافة لدورانها حول الشمس، فكذلك يلف الإلكترون حول نفسه ويدور في نفس الوقت في مدار حول النواة. ويقترن اللف المغزلي للإلكترون بعزم مغناطيسي له، هو الأصل في ظاهرة مغناطيسية المواد

العزم الجيروسكوبي (المدوار): هو حالة خاصة من الحركة حول نقطة ثابتة، يكون فيها عزم العطالة حول أحد محاور العطالة الرئيسي أكبر بكثير من عزم العطالة حول باقي المحاور، بحيث يصبح الاندفاع الزاوي كبيرا حيث لا تؤثر الاضطرابات على الحركة.

منهجية الدراسة

اتبع الباحث منهجية التخطيط العلمي حيث تم برمجة الحلول التحليلية المستنتجة وتمثيل هذه الحلول بيانياً، وكذلك تم استنتاج الحلول العددية لنظام المعادلات وفقاً لما هو مطلوب. وقد تم استخدام هذه المنهجية لدورها في تحليل العديد من المعادلات المتصلة ووصف ما يترتب عليها للوصول إلى النتائج المنشودة من الدراسة

خطوات الدراسة

3-1 تحليل الحركة المغزلية السريعة لجسم متماسك في وجود العزم الجيروسكوبي :

3-1-1 معادلات الحركة وتغيير المتغيرات:

نعتبر جسم متماسك له الكتلة M، مثبت في نقطة واحده  ؛ سطح القصور الناقصي اختياري ويتحرك تحت تأثير مجال قوة نيوتوني مركزي ينشأ من مركز الجذب  الذي يقع في الاتجاه السفلي للمحور الثابت  المار خلال النقطة الثابتة  في وجود مركبة متجه عزم جيروسكوبي  حول المحور z. نعتبر عنصر  عند النقطة  ويقع على مسافة  من نقطة الأصل  و  من النقطة . ( انظر الشكل 1).

المعادلات التفاضلية العامة للحركة وتكاملاتها الأولية هي (Miyazaki et al.، 2008):

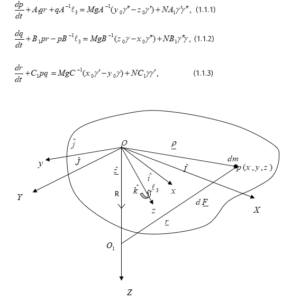
شكل (1) مركبات القوة في الحركة المغزلية

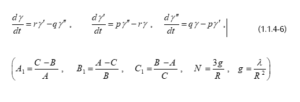
وتكاملاتها الأولية:

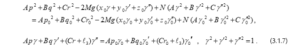
حيث  عزوم القصور الرئيسية للجسم مع اعتبار ،  و  هي احداثيات مركز الكتلة في نظام الاحداثيات المتحرك ، ،  و  هي جيوب التمام الاتجاهية للمحور الثابت في الاتجاه السفلي Z في الهيكل الثابت في الفراغ ، ،  و  هي مساقط متجه السرعة الزاوية للجسم على المحاور الرئيسية للقصور، R هي المسافة من النقطة الثابتة  إلى مركز الجذب ،  معامل الجذب للمركز O₁؛ و ، ، ، ،  و  هي القيم الابتدائية المناظرة للمتغيرات.

كذلك نأخذ في الاعتبار دوران الجسم عند اللحظة الابتدائية حول محور z بسرعة زاويّة عالية  وهذا المحور يصنع زاوية  حيث  مع محور Z. بدون فقد للعمومية، نختار الجزء الموجب للمحور z والمحور x بطريقة ما لتفادي الزاوية المنفرجة مع اتجاه محور Z. طبقاً للقيد على  واختيار النظام الاحداثي نحصل على:

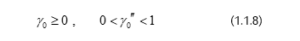
نعرف البارامترات الآتية ( نعتبر البارامترات ):

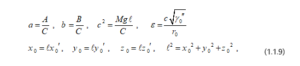
حيث  هو البارامتر الصغير،  كبيره، كذلك ندخل متغيرات جديده

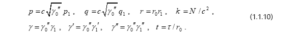
وبالتعويض من(1.1.10) في المعادلات (1.1.1-6) وتكاملاتها(1.1.7)، تصبح:

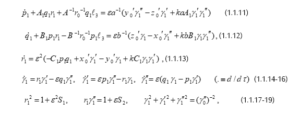
حيث

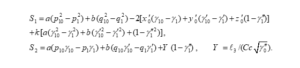
3-1-2 اختزال معادلات الحركة إلى نظام شبه خطي لا يعتمد صراحة على الزمن:

هنا  تكون كبيره، أيضاً ، ، … يمكن إهمالها. بحل المعادلات (1.1.11) و(1.1.14)، نحصل على  و  في الشكل التالي:

نعرف متغيرات جديده  و  (Miyazaki et al., 2008):

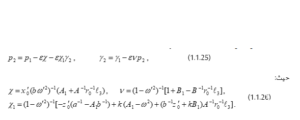
باستعمال (1.1.25)، (1.1.20) و(1.1.24) نحصل على التعابير التالية لـ  و  في حدود متسلسلة القوى في :

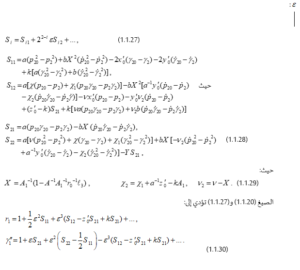
في حدود المتغيرات الجديدة  و ، المتغيرات  و لها الشكل التالي         (1.1.31)

بالتعويض عن (1.1.25)، (1.1.27)، (1.1.28)، (1.1.30) و(1.1.31) في (1.1.21) و(3.1.22)، نحصل على نظام شبه خطي لا يعتمد صراحة على الزمن ذو درجتي حرية كالتالي:

النظام (1.1.32) يمكن الحصول على تكامله الأولي من (1.1.17-19) في الشكل التالي:

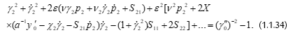
(1.1.34)

هدفنا أن نجد الحلول الدورية لهذا النظام تحت الشروط  أو  ( موجب). في الحالة الأولى، الجسم يدور بسرعة ابتدائية  بالنسبة للمحور الأكبر لسطح القصور الناقصي، بينما في الحالة الثانية الجسم يدور بسرعة ابتدائية  بالنسبة للمحور الأصغر لسطح القصور الناقصي.

3-1-1 صيغة بناء الحلول الدورية:

حيث أن النظام (1.1.32) لا يعتمد صراحة على الزمن فالشروط التالية:

لا تؤثر على عمومية الحلول. النظام المولد لـ (1.1.32) هو

والذي نفترض أن له الحلول الدورية في الشكل التالي:

بدورة .  لكل  ثوابت يمكن تعيينها. نفرض أن الحلول الدورية المطلوبة للنظام الابتدائي المستقل ذاتياً في الشكل التالي:

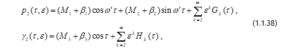
بدورة . الكميات  تمثل انحرافات القيم الابتدائية  للنظام (1.1.32) من قيمهم للنظام (1.1.36) ؛ وهذه الانحرافات دوال في  تتلاشى عندما . نعبر عن الشروط الابتدائية لـ (1.1.38) بالعلاقات الآتية:

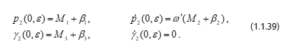
دعنا نعرف الدوال  و    بالمؤثرات

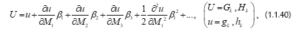
حيث الدوال  و  تعطى في الأشكال التالية:

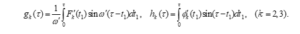
حيث

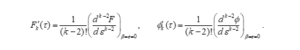
نلاحظ أن الأطراف اليمنى في النظام (1.1.32) تبدأ من الحدود ذات الرتبة  ولذا عندنا:

الآن نحاول إيجاد تعابير الدوال  و . الحلول الدورية (3.1.37) يمكن إعادة كتابتها في الأشكال التالية:

(1.1.41)

حيث

و . باستعمال (1.1.41) و(1.1.28) نحصل على:

(1.1.42)

بالتعويض من (3.1.41) و(3.1.42) في الصيغ (3.1.33) نحصل على:

(1.1.43)

حيث:

(1.1.44)

(1.1.45)

من (1.1.40)، (13.1.43) و(1.1.44) نحصل على النتائج التالية:

(1.1.46)

الثوابت  و  التي تمثل الشروط الابتدائية للحل المولد (1.1.37)، الانحرافات  وتصحيح الدورة  يجب أن تعين من شروط دورية الحلول  ومشتقاتهم الأولى. هذه الشروط يمكن إعادة كتابتها في الشكل التالي:

(1.1.47)

على أي حال، نتيجة لوجود التكامل الأولي (1.1.34) للنظام (1.1.32)، شرط الدورية  غير مستقل. نكتب التكامل (1.1.34) في الصورة:

(1.1.48)

وباستعمال الشرط (1.1.39)، نحصل من المعادلات (1.1.47) على الصورة التالية:

هنا  دالة كاملة في كل المتغيرات، و . إذا كانت ، فمن الصورة (1.1.48) نحصل على:

حيث  دالة كاملة في كل السعات، و . وبالتالي يكون الشرط  من (1.1.47)، يتحقق تلقائياً بتحقق الشروط الأخرى:

(1.1.49)

بالتعويض بالشروط الابتدائية (1.1.39) في التكامل (1.1.34) لـ ، نحصل على المعادلة التالية:

نفرض أن  لا تعتمد على ، نحصل على:

(3.1.50)

ونحصل على كل من  و  من المعادلات (3.1.50) والشرط (3.1.8) في الصورة:

(1.1.51)

حيث  تكون بارامتر اختياري، و  ثابت اختياري موجب. هذا يعني أن الحلول الدورية (1.1.38) تعتمد على ثابت اختياري  والدالة ، والتي تنعدم عندما  تقترب من الصفر. هذه الخصائص لا تعتمد على صورة . تمتد ( تتوسع )الشروط المستقلة للدورية (1.1.47) في متسلسلة قوى لـ  وتحتفظ فقط بالحدود الخطية ( بإهمال الحدود )، وينتج:

وباستعمال القيم الابتدائية (1.1.39) في العلاقات أعلاه، نحصل على الشروط المستقلة للدورية لـ (1.1.49)،

(1.1.52)

باستعمال (1.1.38)، (1.1.51) والمعادلة الأخيرة في (1.1.52)، الدالة  تأخذ الصورة:

(1.1.53)

وبالتالي، بإهمال الحدود من الرتبة  و  في (1.1.52)، نجد أننا حذفنا الحدود ذات الرتبة . باستعمال (1.1.35) و(1.1.39)، سوف نحصل على الحلول الدورية عند السعات الأساسية الصفرية أي أن:

(1.1.54)

باستخدام (1.1.53)، (1.1.54) و(1.1.38)في المعادلتين الأُول من (1.1.52)، نحصل على نظام يعين  و  في الصورة التالية:

استناداً إلى (1.1.46)، النظام أعلاه يتحول إلى:

(1.1.55)

حيث  و  يمكن الحصول عليها من (1.1.45) و(1.1.44)باستبدال  بـ . بواسطة (1.1.23)، (1.1.26)، (1.1.29)، (1.1.44) و(1.1.45)، نحصل على:

حيث:

من الشروط التي على محور  يجب أن يوجه على طول المحور الأكبر أو المحور الأصغر لسطح القصور الناقصي للجسم، يترتب على ذلك  لكل  تحت الاعتبار. نفترض أن:

باستعمال (1.1.55)، التعابير لـ  و  نحصل عليها في شكل متسلسلة قوى في . هذه المفكوكات تبدأ بالحدود ذات الرتب الأعلى من . بالتالي، الحدود الأولى في مفكوكات الحلول الدورية والكمية  تظهر في الصور التالية:

(1.1.56)

(1.1.57)

(1.1.58)

(3.1.59، 60)

(1.1.61)

(1.1.62)

حلولنا (1.1.56-62) معتبره كحالة عامة للحلول المدروسة في (Ismail, 2010) و(Amer et al, 2011) وليس لها نقاط شاذه وبمعنى آخر: الحلول التي حصلنا عليها صحيحة لكل القيم النسبية لـ .

الآن نبحث عن الانحرافات بين حلولنا وكل من الحالة النيوتونية والكلاسيكية، التي تم الحصول عليها في بعض التجارب السابقة الانحرافات يمكن التعبير عنها في الشكل التالي:

وكذلك:

حيث:

1-1-4 التفسير الهندسي للحركة:

في هذا القسم، حركة الجسم المتماسك فُسرت بإدخال زوايا أويلر ، التي يمكن تعيينها من خلال الحلول الدورية التي تم الحصول عليها (انظر الشكل(2)).

حيث أن النظام الابتدائي لا يعتمد صراحة على الزمن، الحلول الدورية لا تزال دورية عند استبدال  بـ ، حيث  فتره زمنية اختيارية. زوايا أويلر، في الحدود التي تحتوي على الزمن ، تعطى في الصور التالية:

(1.1.63)

بالتعويض عن (1.1.56-62) في (1.1.63)، الذي فيه استبدلت  بـ  واستخدام العلاقات (1.1.10)، نحصل على التعابير التالية لزوايا أويلر :

ويمكن اعتبار حالة خاصة من هذه الدراسة وذلك عندما يكون العزم الجيروسكوبي  وسنوضح هذه الحالة في البند التالي:

3-1 الحركة المغزلية السريعة لجسم متماسك عند التردد  و :

في (Amer et al, 2011) تمت دراسة مسألة حركة جسم متماسك حول نقطة ثابتة تحت تأثير مجال جذب نيوتوني عند قيمة التردد الطبيعي . هذا الشذوذ ظهر في (Horton et al.، 2011) واختص بأجسام مختلفة تصنف حسب عزوم القصور الذاتي. وباستخدام طريقة البارامتر الصغير لبوانكريه تم الحصول على الحلول الدورية – ذات سعات صفرية أساسية – للنظام المستقل شبه الخطي في صورة مفكوكات متسلسلات قوى حتى التقريب الثالث وتحتوي على بارامتر صغير افتراضي.

وعندما  تصبح المعادلات (1.1.1-6) في الشكل التالي:

(1.2.1)

(1.2.2)

(1.2.3)

(1.2.4-6)

وتكاملاتها الأولية هي:

(1.2.7)

وهذه المعادلات تختزل إلى النظام شبه الخطي التالي:

(1.2.8)

حيث:

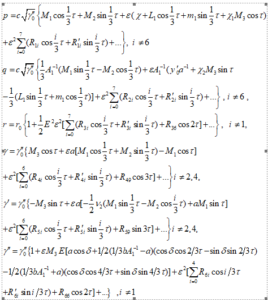
وتكامل أولي:

(1.2.9)

وبتطبيق طريقة البارامتر الصغير لبوانكريه نحصل على الحلول الدورية – ذات السعات الصفرية الأساسية- للنظام المستقل شبه الخطي في صورة مفكوكات متسلسلات قوى حتى التقريب الثالث وتحتوي على بارامتر صغير

افتراضي. وتظهر الحلول في الشكل التالي:

(1.2.10)

حيث  ثوابت يمكن تعينها بالمناظرة مع نظام المعادلات (1.2.8).

ويمكن استنتاج حالة جيروسكوب لاجرانج كحالة خاصة من تلك الحلول وذلك عندما:

وبالتالي تصبح:

1-2-1 التفسير الهندسي للحركة:

تم وصف الحركة باستخدام زوايا أويلر ، التي يمكن تعيينها من خلال الحلول الدورية التي تم الحصول عليها في (1.2.10).

حيث أن النظام الابتدائي لا يعتمد صراحة على الزمن، الحلول الدورية لا تزال دورية عند استبدال  بـ ، حيث  فتره زمنية اختيارية. زوايا أويلر موضحة في العلاقة (1.1.63)

وبفرض اللحظة الابتدائية للزمن تماثل اللحظة  وبالتعويض بالحلول من (3.2.10) في (1.1.63) نحصل على:

المناقشة

عندما يتزامن المحور الصغير للحركات المغزلية للجسم المتماسك مع المحاور الأخرى، يزداد عدد التذبذبات ويقل اتساع الموجات. في الحالة التي لا يوجد فيها عزم الدوران الثابت حول المحور الرئيسي، يكون موضع مركز الجذب مستقلاً بغض النظر عن سلوك الجسم. ويتم عادة تحليل مثل هذه التجارب هندسيا باستخدام زوايا أويلر لوصف اتجاه الجسم في أي لحظة من الزمن بحيث يتم تنفيذ هذه الحلول من خلال برامج الكمبيوتر للحصول على تمثيلاتها الرسومية وتوظيفها في التطبيقات الميكانيكية.

الخاتمة

هدفت هذه الدراسة إلى الحركات المغزلية السريعة لجسم متماسك في مجال قوة نيوتوني في حالة وجود العزم وكذلك في حالة ، وبتطبيق المعادلات الرياضية اللازمة توصلت الدراسة إلى إمكانية إدخال المركبة الثالثة لمتجه العزم الجيروسكوبي  على حركة الجسم واستنتاج تأثير الدوران هذا على الجسم وكذلك تفسيره الهندسي. أيضاً تم علاج جميع الحالات الشاذة التي ظهرت في الأبحاث السابقة التي توقفت عند تفسير الحركة عند مرحلة معينة، وقد تم في هذه الدراسة تفسير الحركة بشكل كامل. وأمكن أيضاً استنتاج جيروسكوب لاجرانج كحالة خاصة جداً من الحلول التي تم الحصول عليها.

قائمة المراجع

• Akulenko، D.، Kozachenko، T. A.، Leshchenko، D. D.، & Zinkevich، Y. S. (2016). Perturbed rotations of a rigid body close to the Lagrange case under the action of unsteady perturbation torques.
• Amer، S. (2008). On the motion of a gyrostat similar to Lagrange’s gyroscope under the influence of a gyrostatic moment vector. Nonlinear Dynamics، 54(3)، 249-262.
• Amer، S.، Ismail، A. I.، & Amer، W. S. (2011). Application of the Krylov-Bogoliubov-Mitropolski technique for a rotating heavy solid under the influence of a gyrostatic moment. Journal of Aerospace Engineering، 25(3)، 421-430.
• Awrejcewicz، ، & Koruba، Z. (2012). Classical mechanics: applied mechanics and mechatronics(Vol. 30). Springer Science & Business Media.
• Chae، (2015). Euler’s equations and the maximum principle. Mathematische Annalen، 361(1-2)، 51-66.
• Cooke، (2012). The Mathematics of Sonya Kovalevskaya. Springer Science & Business Media.
• Horton، ، Sieber، J.، Thompson، J. M. T.، & Wiercigroch، M. (2011). Dynamics of the nearly parametric pendulum. International journal of non-linear mechanics، 46(2)، 436-442.
• Ismail، I. (2010). Motion of a rigid body in a Newtonian field of force exerted by three attracting centers. Journal of Aerospace Engineering، 24(3)، 318-328.
• Leimanis، (2013). The general problem of the motion of coupled rigid bodies about a fixed point(Vol. 7). Springer Science & Business Media.
• Miyazaki، ، Hymanson، H. J.، Morishita، Y.، He، W.، Zhang، H.، Wu، G.، … & Wang، J. C. (2008). Kinematic analysis of the relationship between sagittal alignment and disc degeneration in the cervical spine. Spine، 33(23)، E870-E876.
• Odintsov، D.، & Oikonomou، V. K. (2016). Accelerating cosmologies and the phase structure of F (R) gravity with Lagrange multiplier constraints: A mimetic approach. Physical Review D، 93(2)، 023517.
• Yehia، M. (2015). On the regular precession of an asymmetric rigid body acted upon by uniform gravity and magnetic fields. Egyptian Journal of Basic and Applied Sciences، 2(3)، 200-205.

The Motion of a Rigid Body in the Presence of a Gyrostatic Momentum in Cases of  and