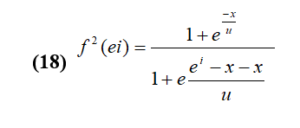Study of the high rotational bands of heavy nuclei (A=190)
by An approach keeping the number of particles

Hamel Fatima zohra                                                                                                                  Djamel Eddine Medjadi

Ecole Normale Supérieure || Kouba || Alger ||  Algérie

DOI PDF

دراسة منطقة الدوران العالية للانوية الثقيلة(A » 190)
باستعمال الحفاظ على عدد الجسيمات

هامل فاطمة الزهراء                                                                                                   جمال الدين مجادي

المدرسة العليا للأساتذة || القبة || الجزائر العاصمة || الجزائر

1-  Introduction :

The theoretical study of the nuclear structure Using Phenomenological interactions- efficient nucleon-nucleon had in the recent decades a lot of success. In this microscopic context, various descriptions of nuclear phenomena have become sufficiently accurate to reach a predictive character and demonstrate their ability to model the nuclear behavior quite well. Such studies include collective rotation modes, especially those concerning the super deformed bands (SD). Constitute the state of the art in the study of rotation bands in heavy nuclei. Numerous calculations have shown that they reproduce quantitatively the properties of the SD bands, in particular at the approximation of A = 190.

that was stadied for different types of collective motion, during the 50 ’and 60 years, the vibrational and rotationl modes were intensely explored within hydrodynamic and quantum frameworkes.in many of theme classical vilocity and current …elds were used in quantum context to describe the collective motion modes, as an exemple, Bohre and motteleson, stadied

the impact of the classicale rotational and internisinc current.this mode interacts with the rotational motion.As for the nuclie, this question was stadied by som autors introducing the Kelvin momentum a semiclassically de…nded quantum operator wich assesses the intrinsc vorticity current.

For many years, various groups have used Hartree-Fock plus BCS (HF+ BCS) or Hartree-Fock Bogoliubov (HFB) solutions moments of inertia, through some variant of the adiabatic time dependent HFB formalism [10]. The region of heavy (A=190) nuclei has been widely studied in this context, in particu- lar for some Hg isotopes by the present authors (see e.g. [11]). A theoretical as well as practical problem is often met in such calculations. It is well known that in such cases the violation of the particle number conservation makes the quasi-particle vacuum approximation quite unsuited and that in most cases the superfluid-normal phase transition is indeed totally spurious. One may meet also there with some computational difficulties upon calculating of the angular velocity of some heavy nuclei, which led to the use of a approach Cr .HTDA which is based on the approach HTDA of by adding a constraint is the angular momentum and angular velocity and through these calculations we get them and from them we cal-culate the determination of moments of inertia on an approach Cr .HTDA

We did this work some static properties nuclei Hg . Pb –pt applying as first study the approximation of “HF+BCS” and then the approximation of “HTDA” as second study with the comparison between the two studies, keeping the particle number, we found that the approximation of “HTDA” is closer then the approximation of “HF+BCS”. To study the rotational properties of these nuclei, we exploit the results obtained by this “HTDA” using another approximation called “Routhein”, this approximation adds a constraint on the kinetic moment that is the angular rate of globules rotation the studied system (cranking operator) in the Hamiltonian, we calculate the rotational energy for the Nuclei Hg-Pb-Pt using the N-N force first and then SKM* and comparing the obtained results.

In is necessary to use microscopical methods to perform investigations taking into accounte the fine effects of the fine effects of the nuclear structure . the HFB model provide a fully selfeonsistent study of the shele and pairing proprities of nuclei.this approache pridects quite well the moments of inertia in super de formed nuclei, for instance combined wich the CrHTDA projection method, it produces better coin cidence with the expremental dynimacal moment of inertia for Hg192 and 194Pb.thus, the Cr HTDA approches are used to describe nuclear systems in the region A=190, the HF, HFB and Cr HTDA calculations were performed for SD-1 band of 192Hg as for the SD-1 band194Pb the SkM⁰ prameterisation for the Skyrme force was used for all calculations

        2-   Rotation models

2.1 The cranking model

The cranking model is one of the most frequently used to describe the Nuclei with high spins. This model describes independent particles in motion in a rotating nucleus, with a distortion and a constant match fields. For this type of system two forces due to rotation appear in the intrinsic reference: the centrifugal force and the Coriolis force. These forces modify the shape and the Nuclei pairing [1]

2.2Angular moment aligned in parallel with the axis of symmetry:

Two interesting cases appear: the pure oblate case, y=60°, and the pure prolate case, y=0°. In the “y=60°” case, the axis of rotation is the axis of symmetry and jx =m is a constant of the movement. Even if there is no collective rotation around the axis of symmetry, every nucleon contributes individually in the total spin I. As long as jx =m is a good quantum number, the eigenfunctions associated with the operators Hw and H0 remain identical. Thereby the Hamiltonian Hw becomes:

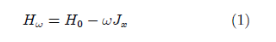
In this case the three operators H0, Jx, Hw commute, therefore they share the same eigenfunctions. We obtain easily the eigenvalues éi of the Hamiltonian Hw :

Where is the projection of the angular momentum perpendicularly at the axis of symmetry of the particle i. The lowest energy of rotating Nuclei possessing N nucleons is by definition the sum of all state energies below the Fermi level:

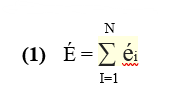
The energy of the fundamental state of the nucleus, E, is given by the expected eigenvalue for the Hamiltonian H0 considering N nucleons in the system:

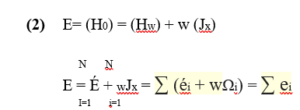
2.3 Transformation of the level schema information into the intrinsic repository:

In order to compare the experimental data contained in a level scheme with the calculations performed in the intrinsic nucleus repository, it is best to transform the level schema information into the rotating repository. The comparison between the behavior of a measured rotational band and the behavior of a modeled band from a given configuration allows reinforcing an interpretation of a band.

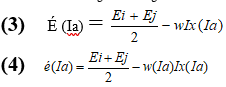
Is the average of  and of

Is the projection of the angular momentum along the axis of rotation that can be obtained by subtracting at the total angular momentum the projection of the angular momentum on the axis of symmetry K according to the theorem of Pythagoras:

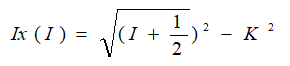
The classical physics relation which allows extracting the angular velocity is:

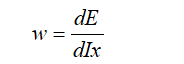
which translates for each transition by the following relation:

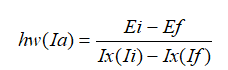
From the previous expression we obtain immediately a quadruple transition when  is less then , the expression , or  is the transition energy. The Routhian total É given by the equation (2.52), includes the energy associated with both heart rotation and quasi-particle excitement. Similarly, the projection  of the total angular momentum on the axis of rotation simultaneously contains a component resulting from the rotation of the heart  (see figure 1). It is preferable to extract the rotational component to obtain the energy . For symmetrical nuclei that rotate around an axis perpendicular to the axis of dissymmetry, is the sum of ( the angular momentum of rotation) and of ( the projection of the angular momentum of the particle on the axis of rotation). The value of is estimated in terms of  From the paired configuration of the fundamental state of even-even nucleus is subtracted from  at the same value of . It is the same to extract the excitation energy from the quasparticle , from the total Routhian, É, and the rotational energy associated with the rotational band of the fundamental state of the even-even nucleus.

FIG (2-1) A vector diagram illustrating the coupling of the angular momentum  of the nucleus with the angular momentum of the nucleus perpendicular to the axis of symmetry, to form the total angular momentum .

2.4 Rotation around a main axis (Cranking approximation):

In this part, our attention will focus on the study of the behavior of rotating nuclei. The “Cranking” model was proposed in 1954 by D. R. Inglis [2]. It consists of considering a nucleus of non-zero angular momentum ( ) moving in a potential rotating at a constant speed  around an axis  {perpendicular to the axis of symmetry of the nucleus. The Schrödinger equation depends on the time regulating this system, expressed in the laboratory reference with the coordinates ( ) (see Fig.2) it’s expressed then as:

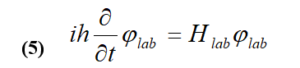
Knowing that the rotation is supposed to be around the

Axis , the projection of the angular momentum  on the axis of rotation is . The rotation operator R is expressed as:

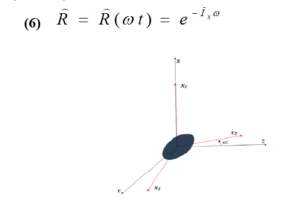
Fig (2-2) Diagram of the coordinates (x, y, z) in the laboratory references and in rotation.

2.5 moment of inertia:

2.5.1 Definition:

In the nucleus the nucleons are in motion, which can generate a collective rotation. The rotational domains can be analyzed by introducing the moment of inertia, which is extracted from the energies of the transitions. By analogy with classical mechanics, recalling the following formulas for the Kinetic moment  and kinetic energy .

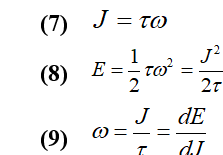
Where is the moment of inertia and is the rotation frequency. The observation of spectra of energy as a function of the spin can reveal the rotational behavior of the nucleus. By analogy with the energy of a rigid body of moment of inertia  in rotation, (9) becomes:

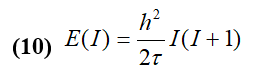
Two quantities comparable to the macroscopic moment  Of inertia can be defined: the moment of dynamic inertia and the moment of cinematic inertia.

-quadruple cascade transitions

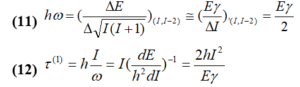
(Where E  measures the energy of excitation of the spin level . In the diagram ( I, E

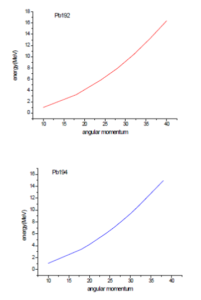
Fig (2-3) the excitation energy  in angular momentum

3-  (The Cranking version of this formalism (Cr.HTDA

We will not describe here the HTDA method that has been described in the usual static case. In Ref[3] to which we refer for an extended presentation. Its basic principles must be kept in the current Routhian approach, in which a linear constraint on the component  of the angular momentum is simply added, thus writing the Routhian in the general form.

Where  is the angular velocity or the multiplier of Lagrange associated with the dynamic constraint , the component of the x-axis of the angular momentum vector, while  is the kinetic energy and is a two-body term consisting of the nucleon-nucleon and Coulomb interactions. Considering a Slater determinant  so far unspecified. Calling the reduction of the body of associated at . We now rewrite as:

It should be noted that the above presentation of disregards the density dependence of the Skyrme interaction being used. Going beyond such a simplification (made here only for the purpose of a clear presentation) would have no practical consequence for the approximate treatment of  discussed below. Formally considering a multipolar expansion of , we will eventually ignore its low multipolar part and simulate the rest, as usual, by a two-body delta interaction. The latter is mainly responsible for pairing-type correlations; the first generates vibrational correlations (of RPA type). Their inclusion in the HTDA framework has been performed elsewhere [18]. The HTDA method consists of solving the static Schrödinger equation for inside a base of holes to very truncated particles. Clearly, the convergence of the solution as a function of depend strongly on the physical relevance of the determinant of ‘Reference’ Slater .

In fact, if is the one-body density matrix associated with the correlated solution (in a somewhat coherent version of HTDA as explained below) or a good approximation, we will take for the fundamental state solution of the Schrödingstatique equation obtained for the operator a body defined with the reduction to a body of (called ) associated to .With this choice, we incorporate in some information about the effects to a body of the correlations present in . It should be noted, by the way, that is therefore different than .

Let’s talk now about the choice made for the interactions in the channel p- h, and in the channels p- ph, h – h. For the first, that is, to define the average fields in the studied area, we chose to use the SkM * interaction [4]. In fact, in the past few decades, it has been amply demonstrated (see for example Ref. [5, 6, 7]) that this Skyrme force was able to describe reasonably average field properties at all degradations in the A 190 mass region as well as fission properties in the actinide mass region.

It can also be noted that since we are dealing here only with pairing correlations neutron-neutron and proton-proton , we will limit here to rotate the singlet states so that x = -1. In practice, the numerical task is simplified by performing truncations at two levels: order  of the particle-hole expansion of the correlated wave function and a limitation of the configuration space to a single particle (sp) in which the states of the particles and holes are considered. Our method is iterative. Each iteration includes the following steps:

1. Given a correlated solution obtained in the previous step, we determine the corresponding density matrix .
2. The resolution of the fundamental state of the one-body operator is used as a vacuum of quasi-particles  (empty for the transformation of simple particle-hole quasi-particles).
3. We build a multi-body base composed of , , , …, states where particle and hole states are constructed relative to in the confined space sp. We stop at a reasonable order n.
4. We calculate in such a base with several truncated bodies, the matrix elements of Vres from  with the replacement of by a null force of  to define  as discussed previously.
5. Finally, we obtain the fundamental state solution of as:

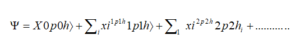
To obtain this solution, we use a standard Lanczos algorithm. In practice, we used the numeric code written by B.N. Parlett and D.S. Scott [8] are available in open source. The energy matrix is diagonal in blocks defined by the symmetries retained. Some details of calculating matrix elements of residual interaction

Residual interaction matrix elements are computed only for sp states belonging to the configuration space. The latter includes sp states whose energies are in the vicinity of the Fermi energy. To avoid any artificial energetic dependency of clean cut (due to the appearance or disappearance of a single particle state in the window by modifying any continuous parameter such as the deformation or the angular velocity), we introduced a usual smoothing factor defined by a cutoff parameter X (here X = 4: 5MeV) and a Smoothing parameter (here, = 0; 5 MeV) given by:

4-          RESULTS AND DISSCUSSION:

We show in Figure. 4-1, 4-2. 4-3 for the Yrast SD bands of the four isotopes considered in this study (196 Os and 198 Pt 196 Hg and 194 Pb) the kinetic moments of the inertia , depending on the angular velocity  for both HFB and RHTDA startup approaches. These calculated values are compared with the experimental results. The HFB results give a rather smooth behavior in reasonable agreement with the data at low angular velocity. However, at higher angular velocities, they differ with experimental velocities. These differences, which are due to abrupt variations of the matching properties as discussed below, do not appear in the results (Cr: HTDA) (RHTDA) which exhibit a regular behavior in good qualitative agreement with the data up to the experimentally higher spin values.

We found that at angular momentum  we find the energy of 5 MeV excitation and that was the experiment It is in the mercury and lead nucleus region (A ~ 190) that the combination of the two factors (excitation energy and minimum angular momentum) seemed the most advantageous for the study of the disquiet of super-trained states A first measurement campaign started at the beginning of the 1990s with the Eurogam multidisciplinary team in its first phase of operation. This is by analyzing the spectrum of all quasisi transitions multinately (in a time interval of a few nanoseconds) with the transitions of the super-formed 192Hg core band, through his change of form to his fundamental spherical state, that we have been able to isolate and characterize for the first time the spectrum of disengagement of a Super-deformed core. It was an almost continuous spectrum spanning a transition energy range of ~ 1 MeV to 4 MeV. By analyzing this spectrum with statistical methods, we have shown that the super deformed nucleus of 192Hg emits on average 3 photons, to evacuate about 4.5 MeV of excitation energy. It has to be at a lower angular momentum.

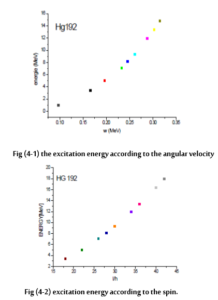
To learn more about the structure of high-spin levels, we drew spin-excitation energy for all bands observed, as shown in Figure 5. Linear behavior is observed until a spin I = 42 Angular momentum

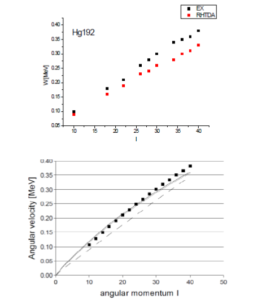
Fig (4-4) the angular velocity related to angular momentum for the bands observed in 192Hg and the bands calculated with the RHTDA model. The experimental bands (calculated) are drawn square. HFB in Continuous line and HF in dashed line.

Linear behavior is observed up to a spin I = 10.40. We observe almost the same angular momentum velocity for the RHTDA model and the experiment as well as between I = 10 and 22 when we find this approximation slightly better than the HFB approximation. Very close to the experiment.

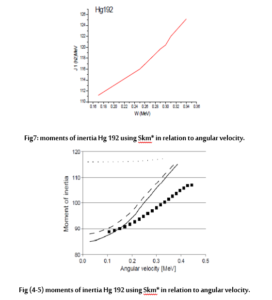
These calculated values are compared with the experimental results. The HFB results give rather smooth behavior, in reasonable agreement with the data at low angular velocities.

However, at higher angular velocities, they disagree with experimental ones. These differences, which are due to the sudden variations of the matching properties described below, do not appear in the RHTDA results that show a regular behavior, in good qualitative agreement with the data, up to the highest known spin values.

We found that when the angular is velocity 0.2and when angular momentum is  we find the energy of the 5 MeV excitements. First high energy transitions (E ~ 10 – 20MeV) these transitions are issued when the energy of disenchantment of the nucleus is very high.

Bands calculated with the RHTDA model. The experimental bands (calculated) are drawn square. HFB in Continuous line and in HF dashed line.

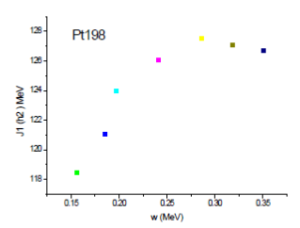
Fig (4-6) moments of inertia Pt 198 using Skm* in relation to angular velocity.

The kinetic moments of inertia , as a function of the angular velocity for both the HFB and RHTDA start approaches. These calculated values are compared with the experimental results. The results of HFB give a rather smooth behavior, in reasonable agreement with the data at low angular velocities.

However, at higher angular velocities, they differ with the experimental ones. These differences, which are due to the sudden variations in the matching properties described below, do not appear in the RHTDA results that show a regular behavior, in good qualitative agreement with the data, up to the highest spin values experimentally known. The kinetic moments of inertia starts from 108 until 122 where the velocity is 0.30 (Mev).

Platinum isotopes are of great interest because they are located in a transitional region. In fact, it is well known that isotopes with A=188 up to A=196 are rather flattened (oblate) the kinetic moments of inertia starts from 118 up to 126 where the velocity is 0.33 (Mev) .

The same phenomenon is observed for the 198Pt isotope. Interesting fact, even if in these two isotopes the proton correlations do not disappear, we note that jumps in the moments of inertia are even more abrupt than those observed in the Hg isotopes.

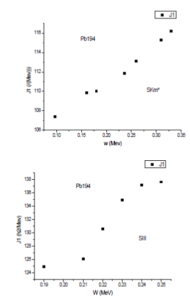
Fig (4-7) moments of inertia Pb194 using Skm* in relation to angular velocity.

Relative to the angular velocity Note that the results of calculating the moments of inertia Hg 192 using Skm* compared to the angular velocity are better than the use of the SKIII force.

 For ¹⁹²Hg

the comparison of the (Cr.HTDA) moments of inertia with the experimental deduced ones shows better reproduction of the experimantal one in comparison with (HF)and (HFB) obtatained.Neverthelss, there is no satisfactory reproduction of the expremental moments of inertia.

 For¹⁹⁴Pb

A good agreement between the cranked HTDA – Skyrme(SkM^{∗})calculations and the exprementally moment of inertia and angular velocity thise ise related to the use for the(SkM^{∗})parameterization OF the Skyrme interaction(to compare with the SIII parameterization case see[9].

Summary and perspectives for futurere earch

This article has presented completely microscopic cranking calculations that explicitly retain the particle count right from the beginning. The HTDA model has been shown to provide a practical approach to doing this. However, as indicated throughout this article, some approximations have proved necessary, They concern the limited analytical form of residual interaction and the restriction of the operating space of several-body waves up to 2p2h excitations. However, the current approach has proved rather effective in addressing some of the major shortcomings of the current description of quasiparticles, especially during rotations leading to a weak match regime. Some of the defects of HFB calculations could be corrected by projection (approximate or exact) on states of exact number of particles. Our method, although it is obviously better in the post-variation projection approach, is in principle equivalent to an exact projection before variation.

To deal with high spin states, Routhian-HTDA calculations are performed using single-particle states of parameter x and parity operators. In Fig. 7, 8 the corresponding results are compared with those obtained in the HFB approaches described above. In the RHTDA approach, the Skyrme force used is the same as the SkM * force that the RHTDA calculations allow to correctly describe (in contradistinction to the HFB approaches) the behavior of the cinematic moments of inertia, the super deformed band of l92Hg, 198 Pt of yrast with strong spins. No superfluid-normal transition is observed. Good results have been obtained for the yrast super deformed l94Pb band using SKM in. It therefore seems that the RHTDA approach is able to better manage the behavior until now of the little reproducible of the extinction of correlation of pairing with very high rotations.

The new approach discussed here opens up the door to a vast area of investigation. In particular, it offers a theoretical framework in which the even nuclei, (odd-odd and odd-even) could be described coherently. An unbalanced breakdown could also be envisaged in the same frame. However, this would require improving the residual interaction used to include its weak multi polar part. Our opinion, the most important task to be accomplished would be to expand the space to the many functions of the body waves in order to improve the description of the correlation correlations. Such work is in progress.

The presented study, especially when it deals with the HTDA framework, is far from being complete. Further investigations and embedding other types of particle- hole excitations in the numerical code may be in order to describe properly the proton-neutron collectivity or at least, to judge their role in this aspect. It is of course unclear what impact on all the results of this work might have broken symmetries, i.e. breaking of the angular momentum symmetry and spurious (due to theBCS approximation) contributions to the breaking of the isospin symmetry. In fact those are current difficulties encountered in mean-field approaches and most of the calculations carried out on extensive scale suffer from both or at least one of these symmetries non-conservation.Despite its possible drawbacks, the HTDA formalism provides a possibility to be applied in many interesting aspects of nuclear physics. From the opposite point of view, they may be a robust test for the presented theory.

Another important issue is the investigation of the high spin states. It is well known that the usual cranked HFB formalism does not “see” the proton-neutron pairing and is not very efficient in the low pairing regime which leads to the discrepancies in the measured and calculated yrast bands. As we mentioned, the treatment of pairing correlations in high spins in the Routhian-HTDA method was already undertaken. Since the rotation has a di®erent impact on like-particle and proton-neutron pairs, it may be judicious to enrich the RHTDA by including the proton-neutron coupling. A great challenge for the (Cr.HTDA)theory would be its application in the β and ββ-decay problems, since it requires a precise knowledge of the ground and several excited states of the parent and granddaughter nuclei, both even-even, plus adetailed description of the intermediate odd-odd nucleus. While first attempts to describe odd nuclei in the HTDA method already have been done, they wait for further development. and also calculate the moment quadripolar of the nucleus of heavy and some rare nuclei in the earth using the approach (Cr.HTDA) and this is important in the row of the nucleus well.

BIBLIOGRAPHY

• BengtssonandJ.D.Garrett, CollectivePheno menain Atomic Nuclei NordicWinterSchool(1983).
• S.Stephens, Rev.Mod.Phys.47, 43(197).
• Pillet, P.Quentin, Libert J.Nucl.PhysAT 697(2002)14.
• , QuentinP., BrackM., GuetC., H.B.Haakansson.Nuc.Phys.A386(1982)79.
• Laftchiev, H., Samsoen, D., Quentin, P, Mikhailov, I.N(2003)Phys.Rev.C, 67, p.014301
• Gall, P.Bonche, J.Dobaczewski .Phys.A348(1994)183.
• (J.Terasaki, P.H.Heenen, P.Dobaczewski, H.Flocard.Nucl.PhyS.A593(1995)1).
• (S.J.Krieger, P.Bonche, H.Flocard, P.Quentin.Nucl.Phys.A517(1990)275).
• (B.N.Parlett, D.N.Scott Math.Comp.33(145)(1979)217.
• (H.Laftchieva, ∗, J.Libertb, P.Quentinc, HaThuyLongd A845, 33-57 2010).
• Quentin, P., Lafchiev, H.Samsoen, D., Mik hailov, I.N (2004)Phys.Rev.C, 69, p. 054315).
• Yuldashbaeva, E., Libert, J., Quentin, P., Girod, M (1999)Phys.Lett.B, 461.
• (L.Prochniak, P.Quentin, M.Imadalou, Int.J.Mod Phys.E21, 1250036(2012).